Содержание
Постановка задания
Задание для всех вариантов звучит так (или, возможно, немного изменено, так как могут быть разные издания учебного пособия):
Алгоритм решения задачи должен быть разделен на две функции: функцию, организующую необходимые вычисления, и функцию main, содержащую операции ввода исходных данных, вызова функции вычисления и вывода результатов.
Создаваемая функция должна иметь возвращаемое значение и список параметров.
Варианты заданий
| Вариант | Задание |
| 1. | В числовую переменную последовательно вводятся целые числа, не равные нулю. Количество вводимых чисел заранее неизвестно. Требуется найти сумму тех введенных чисел, в которых встречаются $n$ заданных цифр. Число цифр $n$ и сама цифра вводятся с клавиатуры. |
| 2. | Среди всех $n$-значных чисел ($n$ задается с клавиатуры) найти числа, запись которых в шестнадцатеричной системе счисления представляет собой палиндром, и подсчитать количество таких чисел (палиндром — число, которое читается одинаково слева направо и справа налево). |
| 3. | Среди простых чисел, не превосходящих заданного натурального числа $N$, найти такое, запись которого в двоичной системе счисления содержит максимальное число единиц. Если таких чисел несколько, найти минимальное число. |
| 4. | Найти все такие простые числа, не превосходящие заданного натурального числа $n$, запись которых в двоичной системе счисления представляет чередующуюся последовательность единиц и нулей, начинающуюся с единицы. |
| 5. | Найти все простые числа, не превосходящие натурального числа $n$, двоичная запись которых представляет собой палиндром; $n$ — задано и не должно превосходить $1000$ (палиндром — число, которое одинаково читается слева направо и справа налево). |
| 6. | Найти все натуральные $n$-значные числа, не превосходящие заданного числа $m$, которые делятся на каждую из своих цифр. Если таких чисел нет, выдать соответствующее сообщение. Произвести проверку вводимой информации. |
| 7. | Найти все натуральные числа $n$, не превосходящие заданного числа $m$ ($0 < m < 20$), такие, что у числа $n! + 5$ $(n! = 1 · 2 · 3 ·\ …\ · n$) сумма цифр — простое число. Если таких чисел нет, выдать соответствующее сообщение. Выполнить проверку вводимой информации. |
| 8. | Среди всех натуральных $n$-значных чисел выбрать и вывести на экран — палиндромы, а также сумму цифр каждого числа (палиндром — числое, которое одинаково читается слева направо и справа налево). |
| 9. | Ввести с клавиатуры границы диапазон $n$ и $m$ натуральных чисел ($n < m$). Из чисел, входящих в этот диапазон, необходимо напечатать только те, цифры которых являются соседними в натуральном ряду. Подсчитать количество этих чисел и определить, сколько среди них четных и нечетных. Предусмотреть проверку правильности ввода информации. |
| 10. | В числовую переменную вводится отличное от нуля целое число. Необходимо вывести на экран цифры этого числа в столбец, начиная со старшего разряда, если это число отрицательное, в противном случае — начиная с младшего разряда. Кроме того, вывести на экран сообщение: четная или нет сумма цифр данного числа. Предусмотреть проверку правильности ввода информации. |
| 11. | В числовую переменную вводится целое число в десятичной системе счисления, имеющее заданное $n$ количество значащих разрядов. Необходимо вывести на экран представление этого числа в двоичной системе счисления. Предусмотреть проверку правильности ввода информации. |
| 12. | В числовую переменную вводится отличное от нуля вещественное десятичное число, меньшее нуля. Необходимо вывести на экран представление этого числа в двоичной системе счисления. Перевод дробной части числа ограничить пятью знаками десятичного числа. Предусмотреть проверку правильности ввода информации. |
| 13. | В числовую переменную вводится отличное от нуля вещественное десятичное число. Необходимо вывести на экран представление этого числа в восьмеричной системе счисления. Перевод дробной части числа ограничить семью знаками. Предусмотреть проверку правильности ввода информации. |
| 14. | Среди всех $n$-значных целых чисел найти числа, запись которых в восьмеричной системе счисления представляет собой палиндром, и подсчитать количество таких чисел (палиндром — число, которое одинаково читается слева направо и справа налево). |
| 15. | Вводятся последовательно цифры. Количество вводимых цифр заранее неизвестно. Из этих цифр составить число таким образом, чтобы цифры числа были расположены в порядке, обратном вводу. Предусмотреть проверку правильности ввода цифровой информации. |
| 16. | Вводятся последовательно цифры. Количество вводимых цифр заранее неизвестно. Из этих цифр составить число таким образом, чтобы цифры числа были расположены в порядке ввода. Предусмотреть проверку правильности ввода цифровой информации. |
| 17. | В числовую переменную вводится отличное от нуля вещественное десятичное число. Необходимо вывести на экран числа, значения сумм цифр целой и дробной частей которого равны между собой. Перевод дробной части ограничить количеством цифр, равным количествую цифр в его целой части. Предусмотреть проверку правильности ввода информации. |
| 18. | Ввести число, содержащее нечетное количество цифр. Из введенного числа сформировать число удалением средних цифр и вывести результат. Предусмотреть проверку правильности ввода чисел с нечетным количеством цифр. |
| 19. | Среди последовательности вводимых натуральных чисел определить количество чисел, содержащих цифру $n$. Количество вводимых цифр заранее неизвестно. Предусмотреть проверку правильности ввода информации. |
| 20. | Дана последовательность из $n$ натуральных чисел. Определить, сколько раз в числах этой последовательности встречалась каждая из цифр. Числа последовательно вводятся в одну переменную. |
| 21. | Дана последовательность натуральных чисел. Найти наибольшую цифру в каждом члене последовательности и их сумму. Числа последовательно вводятся в одну переменную. |
| 22. | Два натуральных числа вводятся с клавиатуры. Число цифр каждого заранее неизвестно. Определить, образуют ли цифры хотя бы одного числа арифметическую прогрессию. Указать вид прогрессии и номер числа. |
| 23. | Дана последовательность чисел, которые вводятся в память в одну переменную. Найти минимальную цифру каждого числа этой последовательности и их произведение. |
| 24. | Для каждого числа из последовательности вводимых $n$ чисел, переставить первую и последнюю цифры и вывести его на печать. |
| 25. | Для каждого числа из последовательности вводимых $n$ чисел прибавить заданную цифру к первой цифре этого числа. |
Лабораторная работа $№5$ предполагает написание программы на языке Си. При заказе работы своего варианта вы получите качественно написанную и хорошо прокомментированную программу.
Дополнительно заказав алгоритм решения вашей задачи (мы крайне рекомендуем это сделать), получите аккуратно оформленный отчет-алгоритм, поясняющий все тонкости решения поставленной задачи.
Образец выполнения (вариант №7)
Условие задания
Найти все натуральные числа $n$, не превосходящие заданного числа $m$ ($0 < m < 20$), такие, что у числа $n! + 5$ $(n! = 1 · 2 · 3 ·\ …\ · n$) сумма цифр — простое число. Если таких чисел нет, выдать соответствующее сообщение. Выполнить проверку вводимой информации.
Алгоритм решения задачи
Прежде чем переходить непосредственно к кодированию данной лабораторной работы, нужно провести ее алгоритмизацию. Данный этап является обязательным и ни один профессиональный программист не опускает его в своей работе.
После прочтения условия становится очевидным, что составители задания требуют от студентов применения плохого стиля программирования. Составители требуют, чтобы было строго лишь $2$ функции:
- главная функция программы (main);
- вычислительная функция (со списком параметров и возвращаемым значением).
💡 Но, если внимательно прочитать условие данной лабораторной, то, очевидно, что нужно ни $2$ функции, а как минимум следующие:
- Ввод с клавиатуры с проверкой на корректность входной информации.
- Нахождение факториала заданного натурального числа.
- Нахождение суммы цифр заданного натурального числа.
- Проверка заданного натурального числа на простоту.
- Главная функция проекта (main).
И это минимум! 😈 Непреложной истиной в программировании является утверждение:
«Одна функция — одно действие«.
Составители же требуют от студентов смешения абсолютно несвязанных операций в рамках одной и той же функции. Разумеется, мы реализуем через $2$ функции данную задачу, но, на наш скромный взгляд и с точки зрения структурного программирования это очень и очень неправильно.
Переходим непосредственно к алгоритмизации данной задачи.
| № | Название операции | Описание операции |
| 1. | Диапазон целых чисел | Допустим, пользователь введет предельное значение $m = 19$, значит, предстоит расчет $19!$ Это огромное число, равное $121\ 645\ 100\ 408\ 832\ 000$. Из целочисленных типов данных языка программирования Си, только тип данных long long может выдержать такой диапазон. Будем использовать именно его, а не какой-нибудь int. |
| 2. | Факториал числа | Факториал натурального числа можно рассчитывать рекурсивно и итерационно. Поскольку для рекурсии требуется отдельная функция, то ничего не остается, как считать факториал в цикле по рекуррентной формуле $n! = n · (n — 1)!$. |
| 3. | Сумма цифр | Для нахождения суммы цифр заданного натурального числа воспользуемся классическим подходом. Будет в цикле получать самый младщий разряд (это самая правая цифра числа) и добавлять его к результирующей сумме. После добавления к сумме, это цифру нужно отбросить, разделив натуральное число на 10. |
| 4. | Простота числа |
Чтобы узнать, является ли заданное натуральное число простым, нужно перебрать всевозможные делители от $2$ до корня из этого числа. Например, нужно узнать, является ли число $29$ простым. Для этого в цикле пробуем разделить нацело число $29$ на следующие числа: $2$, $3$, $4$, $5$. Все, поскольку число $29$ не кратно ни одному из этих чисел, делаем вывод, что оно является простым! Многие зададутся вопросам, а почему проверка делимости заканчивается на $5$. Как было сказано выше, достаточно проверять потенциальные делители до корня из данного числа, то есть до числа $ \leq \sqrt29$, а это значение равно $5$. |
Реализация задачи на языке Си
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 | #include <stdio.h> // для ввода, вывода (scanf, printf) #include <locale.h> // для руссификации (setlocale) #include <conio.h> // задержка программы (getch) #include <math.h> // извлечение корня (sqrt) //-------------------------------------------------- // вычислительная функция // 0 - текущее n не подходит // 1 - текущее n подходит //-------------------------------------------------- int Calculate(const int pm, const int pn, long long *pvalue, int *psumDigit) { int i; // счетчик циклов long long factorial_n; // хранит факториал числа n! long long dvalue; // хранит копию выражения n! + 5 // находим n! итерационно в цикле factorial_n = 1; for(i = 2; i <= pn; i++) factorial_n *= i; // формируем выражение n! + 5 *pvalue = factorial_n + 5; dvalue = *pvalue; // считаем сумму цифр в выражении n! + 5 *psumDigit = 0; while(dvalue != 0) { *psumDigit += dvalue % 10; dvalue /= 10; } // число, равное сумме цифр выражения (n! + 5), проверяем на простоту for(i = 2; i <= sqrt((float)*psumDigit); i++) if(*psumDigit % i == 0) // если число непростое, то обрываем расчеты return 0; return 1; } //-------------------------------------------------- // главная функция программы (точка входа) //-------------------------------------------------- int main(void) { int m; // входное значение int n; // отвечает за искомые значения n int i; // счетчик цикла int count = 0; // количество подходящих n long long value; // хранит выражение n! + 5 int sumDigit; // сумма цифр выражения n! + 5 setlocale(LC_ALL, "rus"); // настройка русскификации в диалогах // запрашиваем с проверкой входное значение m do { printf("Введите значение m из интервала (0 .. 20): "); scanf("%d", &m); } while((m <= 0) || (m >= 20)); // выводим шапку таблицы результатов printf("\nСписок всех натуральных n, удовлетворяющих условию:\n"); printf("\t-------------------------------------------------------\n"); printf("\t| n | n! + 5 | Сумма цифр | Простое |\n"); printf("\t-------------------------------------------------------\n"); for(n = 1; n <= m; n++) { // начинаем все вычисления // если сумма цифр выражения n! + 5 - просто, то выводим результат if(Calculate(m, n, &value, &sumDigit) == 1) { count++; // увеличиваем на 1 кол-во подходящих n printf("\t| %3d | %22lld | %10d | да |\n", n, value, sumDigit); } } printf("\t-------------------------------------------------------\n"); if(count == 0) printf("\t- нет ни одного подходящего значения n"); printf("\n\nДля завершения работы программы нажмите клавишу ENTER..."); getch(); // задержка программы, чтобы можно было просмотреть результат return 0; // завершение работы программы и передача управления в ОС } //-------------------------------------------------- |
Результаты работы программы
| № | Результаты теста |
| 1 | 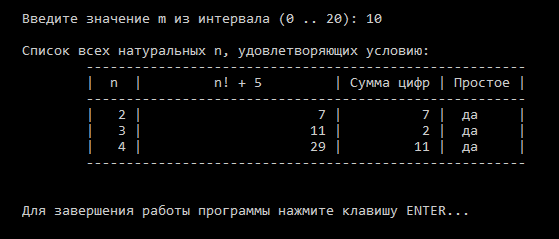 |
| 2 |  |
| 3 | 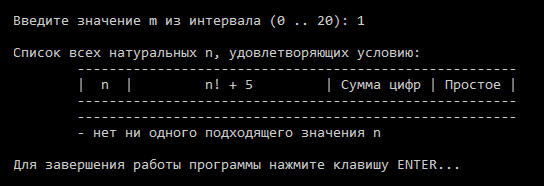 |
Стоимость заказа работы
💡 Стоимость одной программы из любого варианта составляет $200$ рублей.
💡 Стоимость алгоритма (в виде отчета в формате *.doc из любого варианта составляет $200$ рублей (заказывается опционально на ваше усмотрение, чтобы детально разобраться с решением лабораторной работы, например, не прибегая к консультации репетитора).
Для оформления заказа пишите на почту: proglabs@mail.ru.
Время нашего ответа обычно составляет не более 10 минут.
Добавить комментарий