Содержание
Постановка задания
Задание для всех вариантов звучит так (или, возможно, немного изменено, так как могут быть разные издания учебного пособия):
Цель работы: изучение базовых типов данных; разработка алгоритмов и составление программ разветвляющейся структуры.
Варианты заданий
| № вар. | Функция |
| 1. | Найти действительные корни биквадратного уравнения. Предусмотреть выдачу нужных сообщений. |
| 2. | Координаты заданных четырех точек на плоскости соединяются последовательно в порядке перечисления. Найти площадь получившейся фигуры. |
| 3. | Корабль может двигаться четырьмя курсами: на север, на юг, на запад и на восток. Капитан может дать команду на изменение курса: влево, вправо, вперед, назад. Определить новый курс корабля. |
| 4. | Решить систему двух линейных уравнений с двумя неизвестными . Предусмотреть выдачу сообщений: «нет решения», «бесконечное множество решений», «одно решение», «прямые параллельны или перпендикулярны». |
| 5. | Найти координаты точки пересечения прямой $y = kx + b$ и окружности заданного радиуса $r$ с центром в начале координат. В каких координатных четвертях находятся точки пересечения? Если точки пересечения нет или прямая только касается окружности, выдать соответствующее сообщение. |
| 6. | Поле шахматной доски задается парой натуральных чисел, первое из которых задает номер вертикали, а второе — номер горизонтали. Конь расположен на позиции $(a, b)$, а ладья — на $(c, d)$. Определить, угрожает ли конь ладье? Определить также, угрожает ли ладья коню? |
| 7. | Задают координаты трех точек на плоскости, которые последовательно соединяются между собой. Определить тип получаемого треугольника: прямоугольный, остроугольный, тупоугольный. Если треугольник построить нельзя, то сообщить, что точки лежат на одной прямой. |
| 8. | Задаются четыре различных числа: $a, b, c, d$. Выбрать из них три таких числа, которые составляют стороны треугольника наибольшей площади. |
| 9. | Координаты заданных четырех точек на плоскости соединяются последовательно в порядке перечисления. Определить вид получаемой геометрической фигуры: квадрат, прямоугольник, параллелограмм, трапеция, ромб, четырехугольник. |
| 10. | Координаты заданных четырех точек на плоскости соединяются последовательно в порядке перечисления. Является ли полученная фигура выпуклой? |
| 11. | Можно ли из прямоугольного металлического листа размером $a • b$ вырезать две прямоугольные заготовки размерами $c • d$ и $k • p$? Заготовки можно вырезать только параллельно сторонам листа. |
| 12. | С клавиатуры вводится номер года. Напечатать римскими цифрами век, к которому относится данный год. |
| 13. | Координаты заданных трех точек на плоскости соединяются последовательно в порядке перечисления. Определить площадь получаемого треугольника. Вычислить высоты и вывести их на экран в порядке возрастания. |
| 14. | Два прямоугольника, расположенные в первом квадранте, задаются координатами левого верхнего и правого нижнего углов. Вычислить площадь пересечения этих прямоугольников. |
| 15. | Образуют ли прогрессию цифры заданного четырехзначного числа? Определить вид и тип прогрессии. |
| 16. | Два отрезка на плоскости заданы координатами своих концов. Определить, имеют ли эти отрезки общие точки. Отрезки могут располагаться на одной прямой, на параллельных или пересекащихся прямых. |
| 17. | Заданы координаты вершин треугольника на плоскости. Вывести их значения в порядке обхода по часовой стрелке, начиная отсчет угла с оси $OY$. |
| 18. | Четырехугольник задается координатами своих вершин на плоскости. Определить, является ли он выпуклым. |
| 19. | Определить, лежат ли на одной прямой точки с координатами: $(x1; y1)$, $(x2; y2)$, $(x3; y3)$. Если точки лежат на одной прямой, то указать координаты точки, попавшей внутрь отрезка. |
| 20. | Заданы координаты трех вершин треугольника. Вводятся координаты четвертой точки. Определить, внутри или вне треугольника находится эта точка. |
| 21. | Заданы координаты вершин треугольника. Вывести расстояния от начала координат до вершин в порядке обхода против часовой стрелки, ведя отсчет от оси ординат. |
| 22. | Для двух окружностей одинакового радиуса задаются координаты их центров. Определить, пересекаются ли они? Если пересекаются, то вычислить площадь четырехугольника, образуемого центрами окружностей и точками их пересечения. |
| 23. | Координаты двух точек на плоскости задают прямую, которая делит плоскость на две полуплоскости. Вводятся координаты еще двух точек. Определить, принадлежат ли эти точки разным полуплоскостям или они лежат на той же самой прямой? |
| 24. | Поле шахматной доски задается парой натуральных чисел, первое из которых задает номер вертикали, а второе — номер горизонтали. Ферзь расположен на позиции $(a, b)$. Можно ли за один ход попасть на позицию $(c, d)$. Если нет, то как это сделать за два хода? |
| 25. | Определить, является ли палиндромом дробная часть действительного числа, имеющего до четырех значащих цифр? |
Лабораторная работа $№1$ предполагает написание программы на языке Си. При заказе работы своего варианта вы получите качественно написанную и хорошо прокомментированную программу.
Если дополнительно закажите алгоритм решения вашей задачи (мы крайне рекомендуем это сделать), то получите аккуратно оформленный отчет-алгоритм, поясняющий все тонкости решения поставленной задачи.
Образец выполнения (вариант №7)
Условие задания
Задают координаты трех точек на плоскости, которые последовательно соединяются между собой. Определить тип получаемого треугольника: прямоугольный, остроугольный, тупоугольный. Если треугольник построить нельзя, то сообщить, что точки лежат на одной прямой.
Алгоритм решения задачи
Прежде чем переходить непосредственно к кодированию данной лабораторной работы, нужно провести ее алгоритмизацию. Данный этап является обязательным и ни один профессиональный программист не опускает его в своей работе.
Для начала нужно вспомнить, что из себя визуально представляют прямоугольный, остроугольный и тупоугольный треугольники.
| Прямоугольный треугольник | Остроугольный треугольник | Тупоугольный треугольник | |
| Внешний вид |  |  | 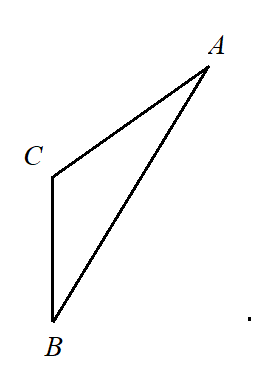 |
| Определ. | Прямоугольный треугольник — треугольник, в котором один угол прямой (то есть $90$ градусов) $\angle C = 90º$ | Остроугольным называют треугольник, у которого все углы острые (то есть меньше $90$ градусов) $\angle A \lt 90º$, $\angle B \lt 90º$, $\angle C \lt 90º$ | Тупоугольным называют треугольник, у которого один из углов тупой (то есть больше $90$ градусов) $\angle C \gt 90º$ |
| Свойство | Сумма квадратов двух сторон равна квадрату его наибольшей третьей стороны (т. Пифагора): $AC^2 + BC^2 = AB^2$. | Сумма квадратов двух сторон больше квадрата его наибольшей третьей стороны: $AC^2 + BC^2 > AB^2$. | Сумма квадратов двух сторон меньше квадрата его наибольшей третьей стороны: $AC^2 + BC^2 < AB^2$. |
💡 То есть, зная длины сторон треугольника, можно однозначно определить его тип!
По условии нам задаются координаты трех вершин треугольника. Найти длины сторон не представляет никакой сложности. Для этого нужно лишь воспользоваться формулой, позволяющей найти расстояние между двумя точками на плоскости.
Если даны две точки $A(x_{1}; y_{1})$ и $B(x_{2}; y_{2})$, то формула имеет вид:
$L = \sqrt{(x_{2} — x_{1})^2 + (y_{2} — y_{1})^2}$.
А вот сейчас важнейший момент алгоритма, разобрав который, сумеем значительно упростить процесс кодирования, сократив количество различных проверок и пр.
Обратите внимание, что во всех этих условиях:
$AC^2 + BC^2 = AB^2$;
$AC^2 + BC^2 > AB^2$;
$AC^2 + BC^2 < AB^2$
нужно знать наибольшую сторону треугольника ($AB$). Понятно, что отыскать ее не составляет никакой сложности, написав соответвующую функцию на языке Си, но при этом придется запомнить оставшиеся $2$ стороны, как ненаибольшие. Проблема в плане кодирования в том, что, используя три переменных для сторон треугольника, неизвестно, какая из них будет выражать наибольшую сторону!
Поэтому применяем следующий прием — к обоим частям выражений добавляем квадрат длины наибольшей стороны:
- $AC^2 + BC^2 + AB^2 = 2·AB^2$ — прямоугольный треугольник;
- $AC^2 + BC^2 + AB^2 > 2·AB^2$ — остроугольный треугольник;
- $AC^2 + BC^2 + AB^2 < 2·AB^2$ — тупоугольный треугольник.
Обратите внимание, что в левой части происходит суммирование всех длин сторон треугольника, а в правой фигурирует лишь наидлинейшая сторона (конкретно в этом примере это сторона $AB$). Алгоритмически это означает, что в процессе кодирования, нам придется отыскать лишь самую длинную сторону и этого будет достаточно.
Также, нужно учесть случай, когда треугольника с заданными вершинами не существует. Опять-таки все это будем рассматривать через призму сторон треугольника, т к это предельно удобно и эффективно.
➡ Условие существования треугольника применительно к нашему случаю: длина наибольшей стороны треугольника должна быть строго меньше суммы двух других сторон треугольника ($AB < AC + BC$).
Необходимые программные функции для кодирования
А теперь давайте выделим функции, которые нам пригодятся в процессе кодирования:
| № | Назначение функции |
| 1 | Считывание координат вершины треугольника. Это можно вынести в отдельную функцию, т к у треугольника $3$ вершины, следовательно, данная операция потребуется трижды. |
| 2 | Нахождение длины стороны треугольника. У треугольника целых $3$ стороны, поэтому данная операция нам потребуется трижды. |
| 3 | Нахождение максимального значения из двух заданных значений. Это функция нам потребуется, когда придется определять самую длинную сторону треугольника. |
| 4 | И последняя функция — функция main(). Данная функция является точкой входой в программы на языке Си, следовательно, она присутствует вообще в любой Си-программе. |
Реализация задачи на языке Си
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 | #include <stdio.h> // для ввода, вывода (scanf, printf) #include <conio.h> // для задержки программы (getch) #include <math.h> // возвдение в степень, извлечения корня, модуль (pow, sqrt, fabs) #include <locale.h> // для руссификации программы (setlocale) #define EPS 0.000001 // точность расчетов //--------------------------------------------------------------------------------------- // структура "Точка на плоскости" //--------------------------------------------------------------------------------------- struct TPoint { int x; // отвечает за значение абсциссы int y; // отвечает за значение ординаты }; //--------------------------------------------------------------------------------------- // ввод с клавиатуры координат текущей точки (А, В или С) //--------------------------------------------------------------------------------------- struct TPoint InputPointCoords(const char* pmessage) { struct TPoint tmp; printf(pmessage); printf("\t- введите координату по оси абсцисс(x): "); scanf("%d", &tmp.x); printf("\t- введите координату по оси ординат(y): "); scanf("%d", &tmp.y); return tmp; } //--------------------------------------------------------------------------------------- // нахождение расстояние между двумя точками на плоскости //--------------------------------------------------------------------------------------- float GetDistanceBetweenPoints(const struct TPoint ppoint1, const struct TPoint ppoint2) { float distance = sqrt(pow((ppoint1.x - ppoint2.x), 2.0) + pow((ppoint1.y - ppoint2.y), 2.0)); return distance; } //--------------------------------------------------------------------------------------- // нахождение максимального из 2-х величин //--------------------------------------------------------------------------------------- float GetMax(const float pa, const float pb) { if(pa > pb) return pa; return pb; } //--------------------------------------------------------------------------------------- int main(void) { struct TPoint a, b, c; // вершины треугольника (А, В, С) float sideAB, sideBC, sideCA; // длины сторон треугольника (АВ, ВС, СА) float sideMax; // самая длинная сторона из всех сторон треугольника float typeTriangle; // позволяет определить тип треугольника setlocale(LC_ALL, "rus"); // руссификация диалогов программы // запрашиваем с клавиатуры координаты всех вершин треугольника a = InputPointCoords("Ввод координат точки А\n"); b = InputPointCoords("\nВвод координат точки B\n"); c = InputPointCoords("\nВвод координат точки C\n"); // вычисляем длины сторон треугольника (AB, BC, CA) sideAB = GetDistanceBetweenPoints(a, b); sideBC = GetDistanceBetweenPoints(b, c); sideCA = GetDistanceBetweenPoints(c, a); // находим самую длинную сторону среди всех сторон треугольника sideMax = GetMax(GetMax(sideAB, sideBC), sideCA); // проверка треугольника на существование // сумма длин меньших 2-х сторон должна быть больше 3-й стороны (a + b > c) // или сумма длин ВСЕХ сторон, должна быть больше удвоенной длины наибольшей стороны (a + b + c > 2c) if(fabs(sideAB + sideBC + sideCA - 2 * sideMax) <= EPS) { printf("\nТреугольник с заданными координатами вершин не существует!"); printf("\nТочки лежат на одной прямой! Программа закрывается..."); getch(); return 0; } // если выполняется условие a^2 + b^2 = c^2 - треугольник прямоугольный // перепишем это условие немного по-другому: a^2 + b^2 + c^2 = 2c^2 - прямоугольный // a^2 + b^2 + c^2 > 2c^2 - остроугольный a^2 + b^2 + c^2 < 2c^2 - тупоугольный typeTriangle = pow(sideAB, 2) + pow(sideBC, 2) + pow(sideCA, 2) - 2 * pow(sideMax, 2); printf("\n\nТреугольник с заданными координатами вершин является: "); if(fabs(typeTriangle) <= EPS) printf("прямоугольным"); else if(typeTriangle > 0) printf("остроугольным"); else printf("тупоугольным"); printf("\nДля завершения работы программы нажмите клавишу ENTER..."); getch(); // задержка программы, чтобы можно было просмотреть результат return 0; // завершение программы и передача управления в ОС } //--------------------------------------------------------------------------------------- |
Результаты работы программы
| № | Тип треугольника | Результат |
| 1 |  |  |
| 2 |  |  |
| 3 |  | 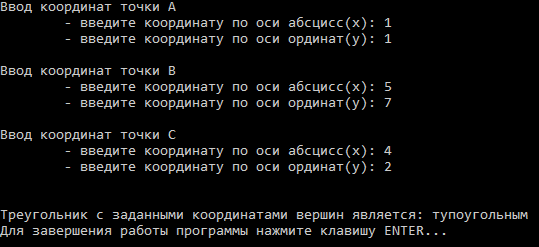 |
| 4 |  | 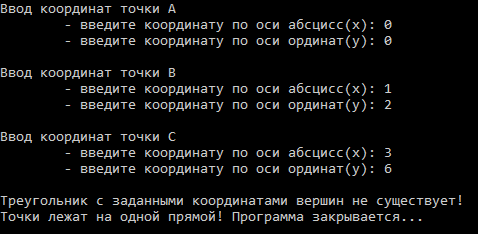 |
Стоимость заказа работы
💡 Стоимость одной программы из любого варианта составляет $200$ рублей.
💡 Стоимость алгоритма (в виде отчета в формате *.doc из любого варианта составляет $200$ рублей (заказывается опционально на ваше усмотрение, чтобы детально разобраться с решением лабораторной работы, например, не прибегая к консультации репетитора).
Для оформления заказа пишите на почту: proglabs@mail.ru.
Время нашего ответа обычно составляет не более 10 минут.
Добавить комментарий