Содержание
Постановка задания
Задание для всех вариантов звучит так (или, возможно, немного изменено, так как могут быть разные издания учебного пособия):
Задана функция на отрезке в виде графика. Задаются произвольный отрезок [a; b] и число табулирования n > 100.
Протабулировать функцию и постранично вывести результат на экран в виде таблицы с «шапкой», состоящей из четырех столбцов: номер точки, аргумент, значение функции, минимальное или максимальное значение.
Найти наименьшее и наибольшее значение функции на отрезке и выделить эти значения в таблице, напечатав их повторно в четвертом столбце. Остальные значения функции на отрезке не повторяются.
Варианты заданий
| Вариант | Графически заданная функция |
| 1 | 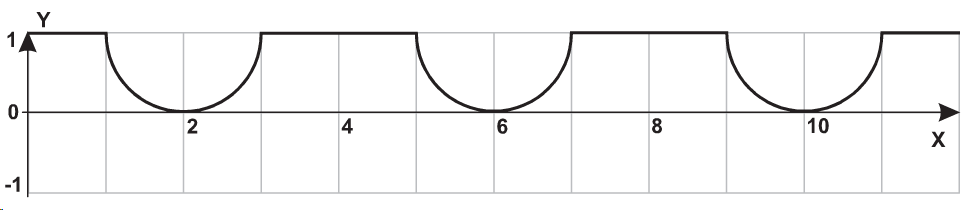 |
| 2 | 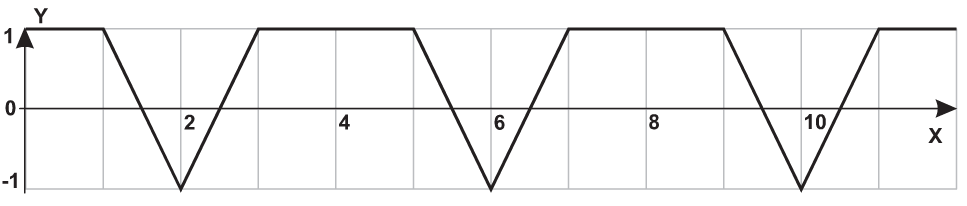 |
| 3 | 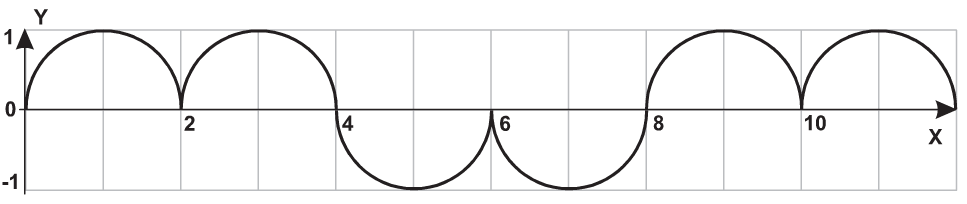 |
| 4 | 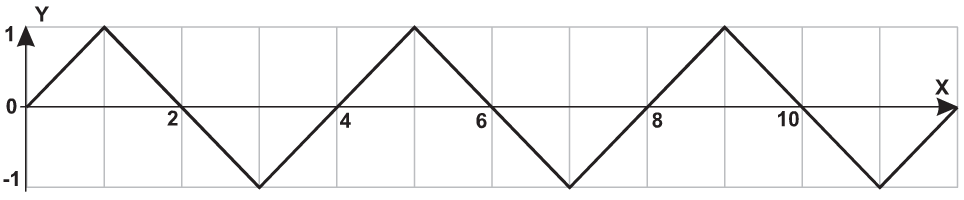 |
| 5 | 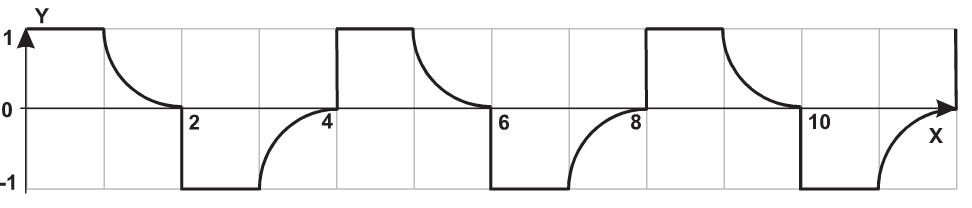 |
| 6 | 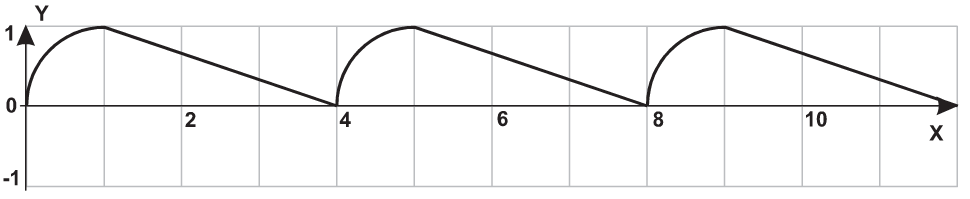 |
| 7 | 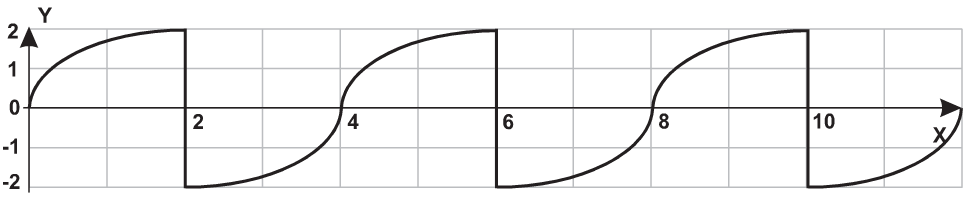 |
| 8 | 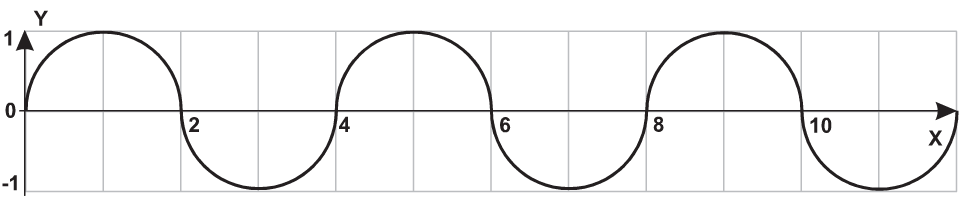 |
| 9 | 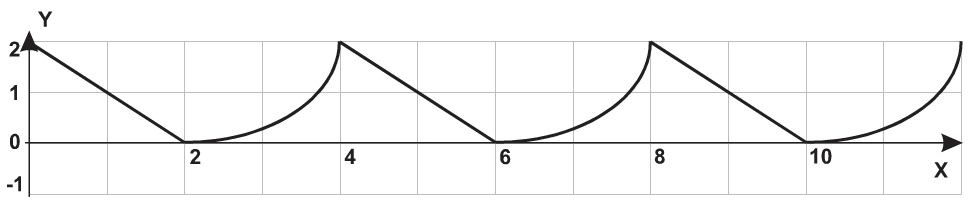 |
| 10 | 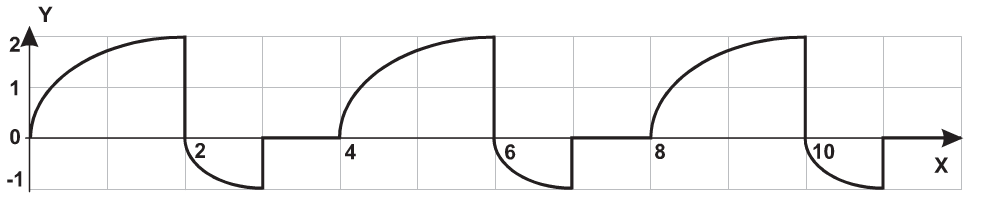 |
| 11 | 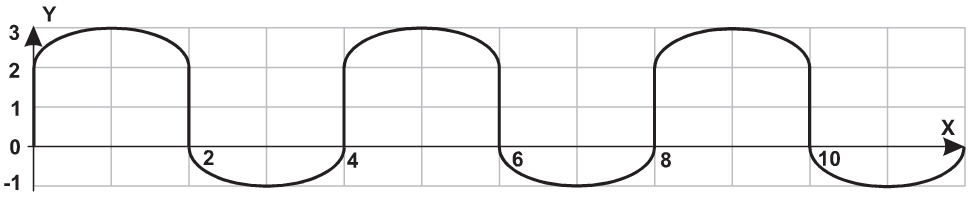 |
| 12 | 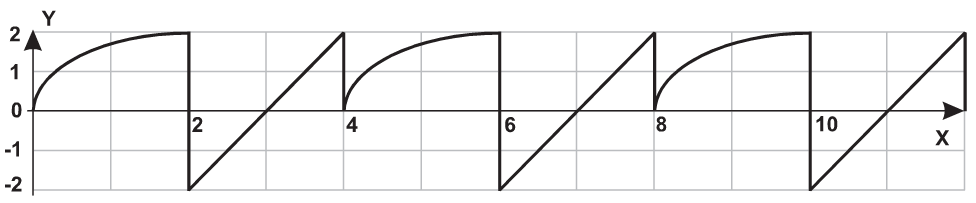 |
| 13 | 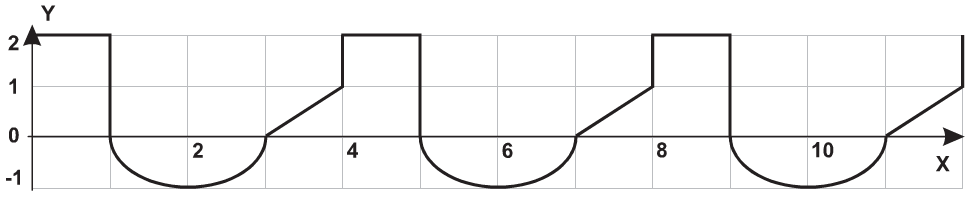 |
| 14 | 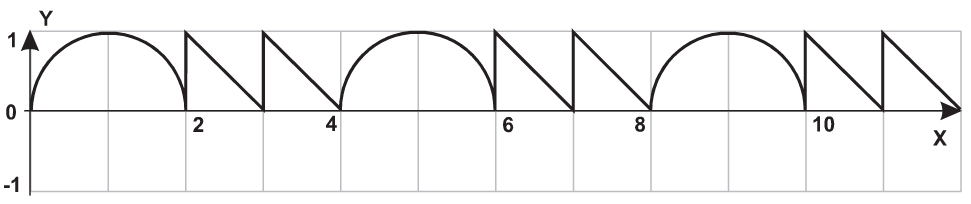 |
| 15 | 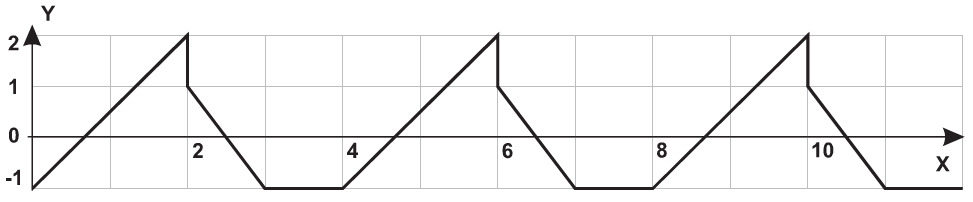 |
| 16 | 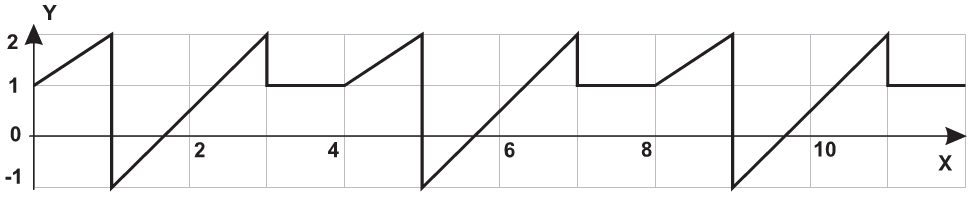 |
| 17 | 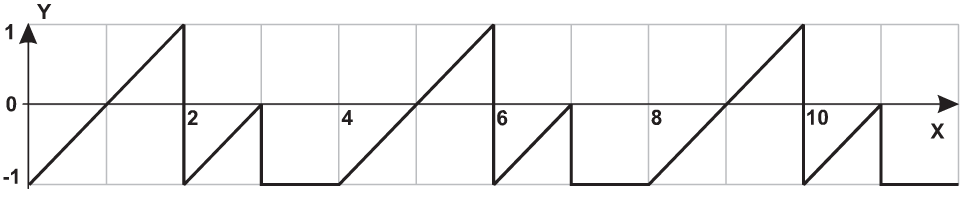 |
| 18 | 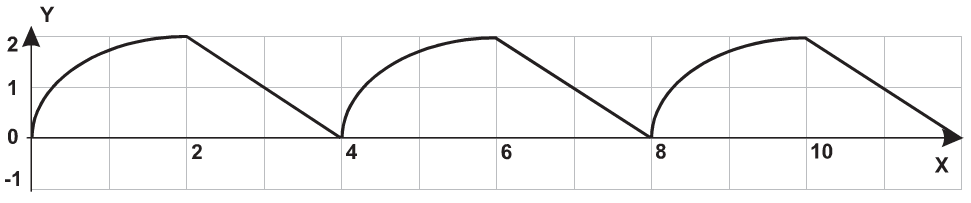 |
| 19 | 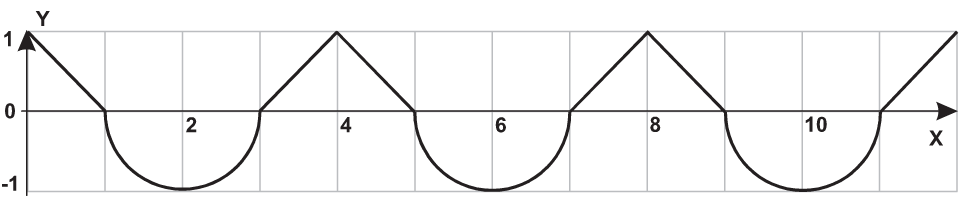 |
| 20 | 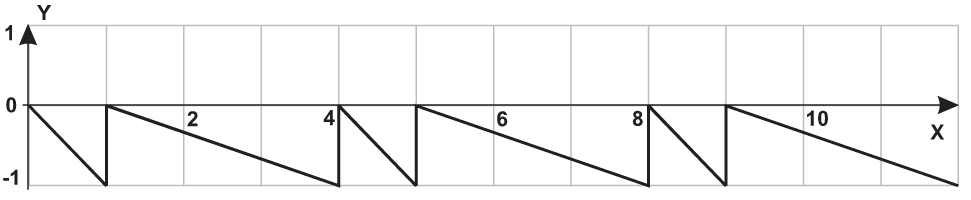 |
| 21 | 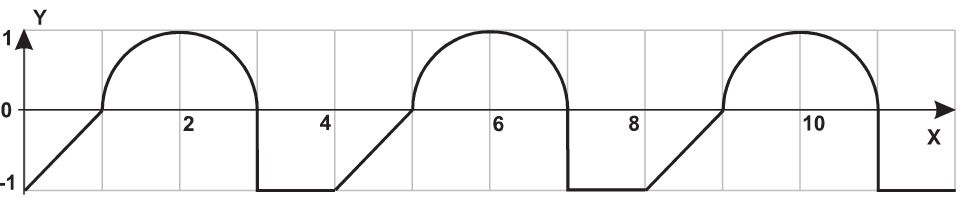 |
| 22 | 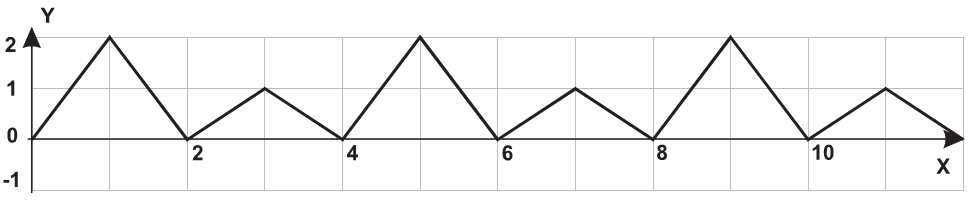 |
| 23 | 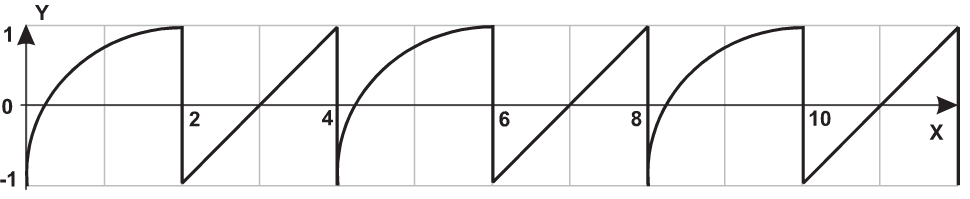 |
| 24 | 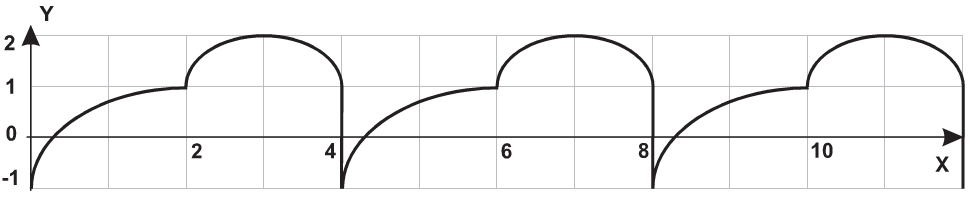 |
| 25 | 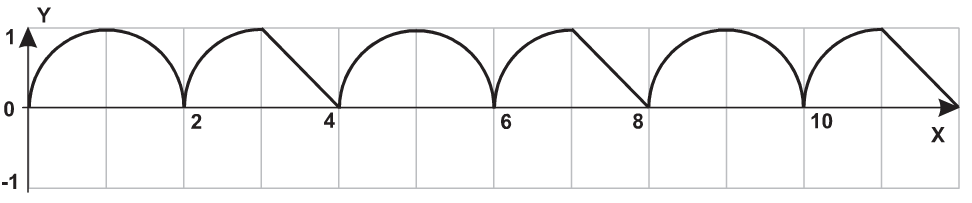 |
Лабораторная работа $№2$ предполагает написание программы на языке Си. При заказе работы своего варианта вы получите качественно написанную и хорошо прокомментированную программу.
Дополнительно заказав алгоритм решения вашей задачи (мы крайне рекомендуем это сделать), получите аккуратно оформленный отчет-алгоритм, поясняющий все тонкости решения поставленной задачи.
Образец выполнения (вариант №1)
Условие задания

Алгоритм решения задачи
Прежде чем переходить непосредственно к кодированию данной лабораторной работы, нужно провести ее алгоритмизацию. Данный этап является обязательным и ни один профессиональный программист не опускает его в своей работе.
➡ Существует несколько способов решения данной задачи. Мы выделили $2$ основных:
- Используя математическую параметризацию.
- Используя математическое проецирование.
Нам показалось, что решать данную задачу через математическое проецирование удобнее и нагляднее, чем через параметризацию, поэтому ниже будет рассмотрен именно $2$-ой способ решения.
Давайте предельно внимательно посмотрим на график заданной функции и сделаем следующие выводы:
- График задан на отрезке $[0; \ 12]$, но это не означает, что мы должны ограничиваться именно этим отрезком. Будем решать в общем виде, то есть рассматривать всю область определения заданной функции: $(-\infty; \ \infty)$.
- Рассматриваемая функция является периодической. Это очень четко прослеживается при тщательном анализе заданного графика функции.
Периодическая фу́нкция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (периода функции) на всей области определения.
- Рассматриваемая функция является четной.
Функция $f(x)$ называется четной, если ее область определения симметрична относительно нуля, и для любого $x$ из области определения выполняется условие: $f(-x) = f(x)$.
- График заданной функции состоит из неразрывно чередующихся геометрических примитивов: горизонтальной линии и полуокружности.
💡 Основная идея математического проецирования применительно к нашей задаче — спроецировать любую точку функции в самый первый (левый) положительный период графика.
Давайте рассмотрим самый левый положительный период графика функции более внимательно.
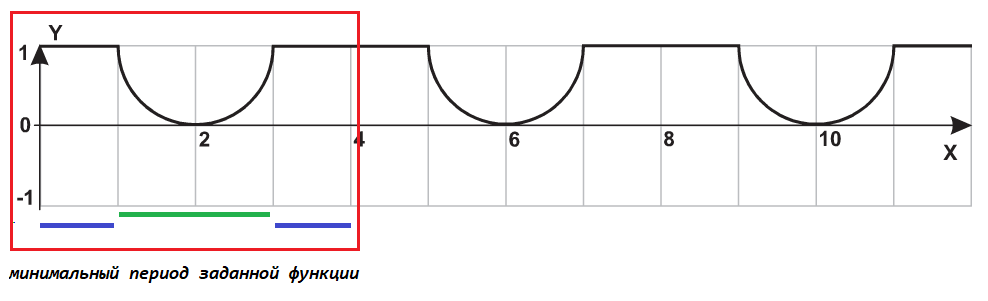
Какие выводы можно сделать после анализа этого фрагмента?
- Длина периода составляет $4$-ре единицы. Другими словами: период состоит из $4$-рех участков.
- Первый и последний участки математически описываются одинаково и представляют собой горизонтальную линию.
- Второй и третий участки также математически описываются одинаково и представляют собой полуокружность (нижнюю часть полноценной окружности).
➡ Давайте запишем уравнения горизонтальной линии и полуокружности.
$f(x) = 2$ — уравнение горизонтальной линии.
$x^2 + y^2 = R^2$ — уравнение окружности с центром в начале координат и радиусом R. Но в нашем примере центр окружности не совпадает с центром начала координат, а имеет смещение на $2$ единицы по оси $Ох$ и на $1$ единицу по оси $Oy$.
Следовательно, для нашей задачи будет актуально следующее уравнение: $(x — 2)^2 + (y — 1)^2 = 1^2$. Но также обязательно нужно учесть, что нас интересует лишь нижняя часть окружности.
➡ Как получать значения нижней полуокружности?
$(x — 2)^2 + (y — 1)^2 = 1^2$
$(y — 1)^2 = 1 — (x — 2)^2$
$y — 1 = \pm\sqrt{1 — (x — 2)^2}$
$y = \pm\sqrt{1 — (x — 2)^2} + 1$
И вот настал момент истинны! Нам необходимо отбирать значения функции, для которых перед корнем стоит знак «$-$». Почему? Да потому что значения из нижней полуокружности меньше значений из верхней полуокружности.
В итоге получаем формульную зависимость для нахождения значений заданной функции, когда подаваемый $x$ попадает во второй или третий участок периода:
$y = -\sqrt{1 — (x — 2)^2} + 1$
Еще раз повторим основную идею алгоритма: независимо от того, какое значение аргумента функции подставляется, нам необходимо перенести его в первый положительный период заданной функции.
Пример №1.
Подставляется $x = 7.5$. Наша цель перенести это значение в первый период, значит $x$ после проецирования будет равен $3.5$.
Пример №2.
Подставляется $x = -2.125$. Так как заданная функция является четной, то мы отбрасываем знак «$-$», получая значение $x = 2.125$, а после этого переносим в первый период. Но это значение итак попадает в первый период изначально, поэтому никаких изменений не происходит.
Пример №3.
Подставляется $x = 173.0625$. Телепортируем $x$ в первый период и получаем значение $x = 1.0625$.
Необходимые программные функции для кодирования
Ниже представлен список необходимых функций, требующихся для успешного решения поставленной задачи (самое главное — помнить о том, что функция должна строго решать какую-то конкретную одну задачу).
| № | Название функции | Назначение функции |
| 1 | FCircle | Вычисляет «меньшую» ординату уравнения окружности $(x — 2)^2 + (y — 1)^2 = 1^2$. |
| 2 | FLine | Получение значения функции $f(x) = 2$. |
| 3 | GetMinFunctionValue | Поиск минимального значения заданной функции на заданном отрезке $[a; b]$. |
| 4 | GetMaxFunctionValue | Поиск максимального значения заданной функции на заданном отрезке $[a; b]$. |
| 5 | F | Происходит проецирование текущего значения $x$ в новое значение, попадающее в первый период заданной функции. В качестве ответа возвращается значение заданной функции. |
| 6 | GetValueFromKeyboard | Ввод какого-либо числа вводом с клавиатуры с ограничением на множество допустимых значений. |
| 7 | PrintTopTable | Вывод «шапки» таблицы результатов на экран. |
| 8 | TabFunction | Происходит табулирование заданной функции на заданном отрезке $[a; b]$ при заданном количество разбиений $n$. |
| 9 | main | Главная функция программы (точка входа). |
Итого получилось $9$ функций. Каждая из этих функций выполняет строго одно действие и это важнейший момент правильного программирования.
Реализация задачи на языке С
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 | #include <stdio.h> // для консольного ввода-вывода (scanf-printf) #include <math.h> // для математических функций (sqrt, pow) #include <conio.h> // для задержки работы программы (getch) #include <stdlib.h> // для очистки экрана от последних выводов (cls) double F(const double px); // опережающее описание функции //----------------------------------------------------------------------------------- // уравнение окружности (x - 2)^2 + (y - 1)^2 = 1^2 // с центром в точке {2; 1} и радиусом R = 1 double FCircle(const double px) { // раздел объявления констант const short int R = 1.0; // радиус окружности const short int Xcenter = 2; // абсцисса центра окружности const short int Ycenter = 1; // ордината центра окружности // раздел объявления переменных double y; // хранит значение функции при заданном аргументе px // раздел вычислений // (y - Ycenter)^2 = R - (x - Xcenter)^2 // y = +-sqrt(R - (x - Xcenter)^2) + Ycenter // берем со знаком "-", т к нас интересуют "нижние" значения окружности y = -sqrt(R - pow(px - Xcenter, 2.0)) + Ycenter; return y; } //----------------------------------------------------------------------------------- // уравнение прямой линии, параллельной оси Ох double FLine(void) { return 1; } //----------------------------------------------------------------------------------- // поиск минимального значения функции на заданном отрезке [a; b] // pa - левая граница отрезка [a; b] // pb - правая граница отрезка [a; b] // pn - количество разбиений отрезка [a; b] double GetMinFunctionValue(const double pa, const double pb, const long pn) { long i; // счетчик цикла double x; // текущее значение аргумента функции double dx; // приращение аргумента функции х double minValue; // хранит минимальное значение функции double currentValue; // текущее значение функции dx = (pb - pa) / (double)pn; // находим приращение х при табулировании функции // предполагаем, что в точке (а) функция имеет наименьшее значение minValue = F(pa); // в цикле начинаем табулировать функцию с шагом dx for(i = 1; i <= pn; i++) { x = pa + dx * i; currentValue = F(x); // если текущее значение функции (в точке х) меньше, чем любое из ранее найденных значений, то if(currentValue < minValue) minValue = currentValue; // запоминаем новое минимальное значение } return minValue; // в качестве ответа возвращаем наименьшее значение функции на отрезке [a; b] } //----------------------------------------------------------------------------------- // поиск максимального значения функции на заданном отрезке [a; b] // pa - левая граница отрезка [a; b] // pb - правая граница отрезка [a; b] // pn - количество разбиений отрезка [a; b] double GetMaxFunctionValue(const double pa, const double pb, const long pn) { long i; // счетчик цикла double x; // текущее значение аргумента функции double dx; // приращение аргумента функции х double maxValue; // хранит максимальное значение функции double currentValue; // текущее значение функции dx = (pb - pa) / (double)pn; // находим приращение х при табулировании функции // предполагаем, что в точке (а) функция имеет наибольшее значение maxValue = F(pa); // в цикле начинаем табулировать функцию с шагом dx for(i = 1; i <= pn; i++) { x = pa + dx * i; currentValue = F(x); // если текущее значение функции (в точке х) больше, чем любое из ранее найденных значений, то if(currentValue > maxValue) maxValue = currentValue; // запоминаем новое максимальное значение } return maxValue; // в качестве ответа возвращаем наибольшее значение функции на отрезке [a; b] } //----------------------------------------------------------------------------------- // в этой функции происходит проецирование текущего значения аргумента функции в значение аргумента из 1го периода // в качестве ответа возвращается значение функции из 1го периода функции double F(double px) { double y; // отвечает за значение функции long integerPartOfDoubleNumber; // целая часть вещественного числа double fractionalPartOfDoubleNumer; // дробная часть вещественного числа short int part; // отвечает за анализируемый фрагмент функции // новое значение аргумента, подставляемое в уравнение окружности (x - 2)^2 + (y - 1)^2 = 1^2 double newx; // т к заданная функция явялется четной f(-x) = f(x), то необходимо избавиться от знака "-", если он есть px = (px < 0) ? -px : px; integerPartOfDoubleNumber = (int)px; fractionalPartOfDoubleNumer = px - integerPartOfDoubleNumber; part = integerPartOfDoubleNumber % 4; switch(part) { case 0: case 3: { y = FLine(); break; } case 1: case 2: { newx = fractionalPartOfDoubleNumer + part; y = FCircle(newx); break; } } return y; } //----------------------------------------------------------------------------------- // ввод границ отрезка табулирования или кол-ва разбиений данного отрезка double GetValueFromKeyboard(const long pa, const long pb, char* pmessage) { double result; do { printf(pmessage, pa, pb); scanf("%lf", &result); } while((result < pa) || (result > pb)); return result; } //----------------------------------------------------------------------------------- // вывод шапки табличного вывода на экран // pa - левая граница отрезка [a; b] // pb - правая граница отрезка [a; b] // pn - количество разбиений отрезка [a; b] void PrintTopTable(const double pa, const double pb, const long pn) { // номер страницы табличного вывода // при каждом вызове данной функции кол-во страниц вывода будет увеличиваться на 1 static long pageNumber = 0; pageNumber++; printf("Табулирование графически заданной функции на отрезке [%.4lf .. %.4lf] (n = %d - количество разбиений)\n", pa, pb, pn); printf("\t\t\t\t\t\t - стр.№%ld - \n", pageNumber); // ╚╔ ╩ ╦ ╠ ═ ╬ ╣ ║ ╗ ╝ символы псевдографики для построения красивого каркаса таблицы при выводе // выводим шапку таблицы printf("\t\t\t╔═════════╦══════════════╦══════════════════╦══════════════════╗\n"); printf("\t\t\t║ № точки ║ аргумент ║ значение функции ║ минимум/максимум ║\n"); printf("\t\t\t╠═════════╬══════════════╬══════════════════╬══════════════════╣\n"); } //----------------------------------------------------------------------------------- // функция, в которой происходит табулирование заданной функции с выводом результатов на экран // pa - левая граница отрезка [a; b] // pb - правая граница отрезка [a; b] // pn - количество разбиений отрезка [a; b] void TabFunction(const double pa, const double pb, const long pn) { #define EPS 0.000001 // точность всех расчетов одна миллионная double minValue = GetMinFunctionValue(pa, pb, pn); // хранит минимальное значение функции на отрезке double maxValue = GetMaxFunctionValue(pa, pb, pn); // хранит максимальное значение функции на отрезке double x; // значение аргумента табулирумой функции double dx; // шаг приращения аргумента функции long i; // счетчик цикла, а также по совместительсту и №точки double y; // значение функции в точке x dx = (pb - pa) / (double)pn; // вычисляем шаг приращения аргумента функции PrintTopTable(pa, pb, pn); // выводим шапку таблицы на экран // начинается главный процесс табулирования функции for(i = 0; i <= pn; i++) { x = pa + dx * i; y = F(x); // выводим информацию о текущей точке функции printf("\t\t\t║ %7d ║ %12.6lf ║ %16.6lf ║", (i + 1), x, y); // если текущее значение функции совпадает с минимальным/максимальным, то выводим его повторно в 4ую колонку if(fabs(y - minValue) <= EPS) printf(" %16.6lf ║\n", y); else if(fabs(y - maxValue) <= EPS) printf(" %16.6lf ║\n", y); else printf(" %16s ║\n", ""); // т к требуется постраничный вывод if((i + 1) % 20 == 0) // заканчивается текущая страница { printf("\t\t\t╚═════════╩══════════════╩══════════════════╩══════════════════╝\n"); printf("Для перехода к следующей странице вывода нажмите ENTER..."); getch(); // и начинается новая страница вывода PrintTopTable(pa, pb, pn); } } printf("\t\t\t╚═════════╩══════════════╩══════════════════╩══════════════════╝\n"); } //----------------------------------------------------------------------------------- // главная функция программы (точка входа) void main(void) { double a, b; // границы отрезка табулирования заданной функции long n; // количество разбиений отрезка табулирования a = GetValueFromKeyboard(-1000, 1000, "Введите левую границу отрезка для табулирования функции [%ld ... %ld]: "); b = GetValueFromKeyboard(-1000, 1000, "Введите правую границу отрезка для табулирования функции [%ld ... %ld]: "); n = (long)GetValueFromKeyboard(101, 10000, "Введите кол-во разбиений отрезка табулирования функции [%ld ... %ld]: "); TabFunction(a, b, n); // начинается табулирование функции printf("\n\nДля завершения работы программы нажмите ENTER..."); getch(); // задержка программы, чтобы можно было просмотреть результаты } //----------------------------------------------------------------------------------- |
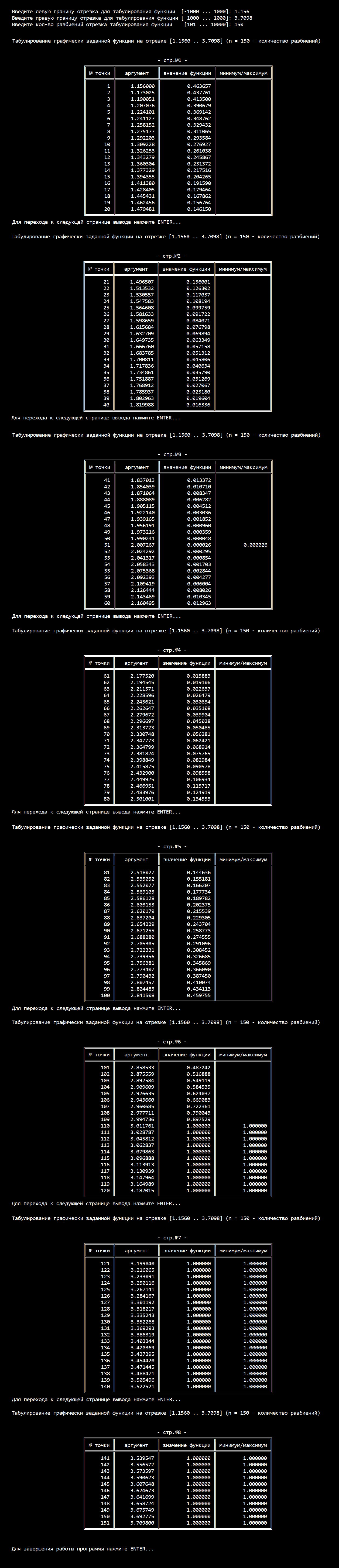
Результаты работы программы
Стоимость заказа работы
➡ Стоимость программы из любого варианта составляет $250$ рублей.
➡ Стоимость детального алгоритма из любого варианта составляет $300$ рублей (заказывается опционально на ваше усмотрение, чтобы детально разобраться с решением лабораторной работы, например, не прибегая к консультации репетитора).
Также дополнительно вы можете заказать у нас:
- Построение аккуратной ГОСТовой блок-схемы. Ориентировочная стоимость $250$ рублей.
- Отчет о проделанной работе (иногда в вузах есть требование — предоставить отчет к лабораторной работе). Ориентировочная стоимость $200$ рублей.
Для оформления заказа пишите на почту: proglabs@mail.ru.
Время нашего ответа обычно составляет не более $10$ минут.
Добавить комментарий