Содержание
| ВНИМАНИЕ | Для получения программы своего варианта пишите на наш электронный адрес proglabs@mail.ru |
Варианты задания №1
💡 Во всех заданиях использовать только простые циклы
| № | Условие |
| 1 | Вычислить для первых $20$ значений $X = \frac{1}{2},\ 1\ -\ \frac{2}{3},\ 1\ -\ \frac{3}{4},\ …$ и вывести в виде таблицы с заголовками:
Для организации цикла использовать оператор for. При вычислениях приближенных значений использовать только операции сложения, вычитания, умножения, деления. |
| 2 | Вычислить при $X = (-0.5;\ -0.25;\ 0;\ 0.25;\ 0.5;\ 0.75;\ 1)$ и вывести в виде таблицы с заголовками:
Для организации цикла использовать оператор while. При вычислениях приближенных значений использовать только операции сложения, вычитания, умножения, деления. |
| 3 | Вычислить при $X$, изменяющемся от $0.1$ до $\frac{\pi}{3}$ с шагом $0.05$, и вывести в виде таблицы с заголовками:
Для организации цикла использовать оператор for. При вычислениях приближенных значений использовать только операции сложения, вычитания, умножения, деления. |
| 4 | Вычислить в цикле do-while при $X$, изменяющемся от $0$ до $\frac{\pi}{4}$ с шагом $0.1$, и вывести в виде таблицы с заголовками:
При вычислениях приближенных значений использовать только операции сложения, вычитания, умножения, деления. |
| 5 | Вычислить при $X$, изменяющемся от $A$ до $B$ с шагом $H$, и вывести в виде таблицы с заголовками:
Для организации цикла использовать оператор for. При вычислениях приближенных значений использовать только операции сложения, вычитания, умножения, деления. |
| 6 | Вычислить при $M$, изменяющемся от $0$ до $6$ с шагом $0.5$, и вывести в виде таблицы с заголовками:
Для организации цикла использовать оператор while. При вычислениях приближенных значений использовать только операции сложения, вычитания, умножения, деления. |
| 7 | Вычислить при $X = (1;\ 0.5;\ 0.25;\ 0.125;\ 0.0625;\ 0.03125;\ 0.015626)$ и вывести в виде таблицы с заголовками:
Для организации цикла использовать оператор for. При вычислениях приближенных значений использовать только операции сложения, вычитания, умножения, деления. |
| 8 | Вычислить при $X = \sin(5^\circ),\ \sin(10^\circ),\ …,\ \sin(60^\circ)$ и вывести в виде таблицы с заголовками:
Для организации цикла использовать оператор for. При вычислениях приближенных значений использовать только операции сложения, вычитания, умножения, деления. |
| 9 | Вычислить в цикле do-while при первых $15$ значениях $X = \tan(\frac{1}{2}45^\circ),\ \tan(\frac{1}{3}45^\circ),\ \tan(\frac{1}{4}45^\circ),\ …$ и вывести в виде таблицы с заголовками:
При вычислениях приближенных значений использовать только операции сложения, вычитания, умножения, деления. |
| 10 | Вычислить при $X$, изменяющемся от $X_0$ до $X_1$ с шагом $H$, и вывести в виде таблицы с заголовками:
Для организации цикла использовать оператор for. При вычислениях приближенных значений использовать только операции сложения, вычитания, умножения, деления. |
| 11 | Для функции $Y = \frac{X e^{-X^2}}{1\ +\ X}$ и вводимого значения $X$ вычислить:
Для организации цикла использовать оператор while. Результаты вычислений и соответствующие значения $DX$ вывести в виде таблицы с заголовками столбцов. |
| 12 | Для функции $Y = \frac{1\ +\ 2X}{X^2\ -\ 1}$ и вводимого значения $X$ вычислить:
Для организации цикла использовать оператор for. Результаты вычислений и соответствующие значения $DX$ вывести в виде таблицы с заголовками столбцов. |
| 13 | Для функции $Y = \frac{\ln(1\ +\ \cos(X))}{2^X\ +\ 1}$ и вводимого значения $X$ вычислить:
Для организации цикла использовать оператор for. Результаты вычислений и соответствующие значения $DX$ вывести в виде таблицы с заголовками столбцов. |
| 14 | Для функции $Y = \frac{2^X}{1\ +\ \ln(2\ +\ \cos(X))}$ и вводимого значения $X$ вычислить:
Для организации цикла использовать оператор for. Результаты вычислений и соответствующие значения $DX$ вывести в виде таблицы с заголовками столбцов. |
| 15 | Для функции $Y = \ln(1\ +\ X^2) \tan(X^2)$ в точке $X = 0.3$ вычислить:
И вывести полученные значения и соответствующие значения $DX$ в виде таблицы с заголовками столбцов. |
| 16 | Для функции $Y = \frac{\sin(X)}{\ln(2\ +\ \sin^2(X)}$ и вводимого значения $X$ вычислить:
И вывести полученные значения и соответствующие значения $DX$ вывести в виде таблицы с заголовками столбцов. |
| 17 | Для функции $Y = \arctan(\sqrt{\frac{X\ +\ 1}{1\ -\ X}})$ и вводимого значения $X$ вычислить:
И вывести полученные значения и соответствующие значения $DX$ в виде таблицы с заголовками столбцов. |
| 18 | Для функции $Y = \frac{X\ +\ 1}{(X\ +\ 2)(X\ +\ 3)}$ и вводимого значения $X$ вычислить:
И вывести полученные значения и соответствующие значения $DX$ в виде таблицы с заголовками столбцов. |
| 19 | Упростив вычисления за счет использования дополнительных переменных и/или скобочных форм, вычислить в цикле do-while значения функции $Y = \frac{\tan^4(X)}{4}\ -\ \frac{\tan^2(X)}{2}\ -\ \ln(\cos^2(X))$ и ее производной $Y'(X) = \frac{\tan^3(X)}{\cos^2(X)}\ -\ \frac{\tan(X)}{\cos^2(X)}\ -\ 2\tan(X)$ на интервале от $-7.5^\circ$ до $+7.5^\circ$ с шагом $0.75^\circ$. Для проверки правильности результата вычислить также значение производной по заданной формуле без преобразований. Найденные значения вывести в виде таблицы с предшествующими порядковым номером и соответствующим значением аргумента $X$. |
| 20 | Упростив вычисления за счет использования дополнительных переменных и/или скобочных форм, вычислить значения функции $Y = (\frac{X\ -\ 1}{2}\ -\ \frac{(X\ -\ 1)^2}{2}\ +\ \frac{(X\ -\ 1)^4}{3})(X^2\ -\ 1)$ и ее производной $Y'(X) = (\frac{1}{2}-(X-1)\ +\ \frac{4(X-1)^3}{3})(X^2-1)\ +\ (\frac{X\ -\ 1}{2}-\frac{(1\ -\ X)^2}{2}+\frac{(1\ -\ X)^4}{3})2X$ на интервале от $-1.1$ до $+1.0$ с шагом $0.1$. Для проверки правильности результата вычислить также значение производной по заданной формуле без преобразований. Найденные значения вывести в виде таблицы с предшествующими порядковым номером и соответствующим значением аргумента $X$. Для организации цикла использовать оператор for. |
| 21 | Для функции $F = \frac{2X(1\ -\ X)\ +\ (1\ +\ X^2)}{2(1\ -\ X)^2}\sqrt{\frac{1\ -\ X}{1\ +\ X^2}}$ при $X = 0.5$ и $K$ приращениях аргумента $DX = (0.0005;\ 0.001;\ 0.002;\ 0.004;\ 0.008;\ …)$ вычислить:
Результаты вычислений и соответствующие значения $DX$ вывести в виде таблицы с заголовками столбцов. Для организации цикла использовать оператор while. |
| 22 | Для функции $F = \frac{e^x\ -\ e^{-x}}{e^x\ +\ e^{-x}}$ и вводимого значения $X$ при $N$ приращениях аргумента $DX = (-0.1;\ \frac{-0.1}{4};\ \frac{-0.1}{16};\ …)$ вычислить:
Результаты вычислений и соответствующие значения $DX$ вывести в виде таблицы с заголовками столбцов. Для организации цикла использовать оператор for. |
| 23 | Для функции $F = \frac{\sin^3(X)\ +\ 1}{\sin^2(X)}$ и вводимого значения $X$ при приращениях аргумента $DX = (-0.0005;\ +0.001;\ -0.002;\ +0.004;\ -0.008;\ +0.016)$ вычислить:
Результаты вычислений и соответствующие значения $DX$ вывести в виде таблицы с заголовками столбцов. Для организации цикла использовать оператор for. |
| 24 | Для функции $F = \frac{-2Xe^{-X^2}}{1\ +\ e^{-X^2}}$ и вводимого значения $X$ при $K$ приращениях аргумента $DX = (-0.0005;\ -0.001;\ -0.002;\ -0.004;\ …)$ вычислить в цикле do-while:
Результаты вычислений и соответствующие значения $DX$ вывести в виде таблицы с заголовками столбцов. |
| 25 | Для функции $F = \frac{2}{(2X\ -\ 1)^2 \sqrt{1\ -\ (\frac{1}{2X\ -\ 1})^2}}$ при $X = 1.5$ и $K$ приращениях аргумента $DX = (5 \cdot 10^{-1};\ 5 \cdot 10^{-2};\ 5 \cdot 10^{-3};\ 5 \cdot 10^{-4};\ …)$ вычислить:
Результаты вычислений и соответствующие значения $DX$ вывести в виде таблицы с заголовками столбцов. Для организации цикла использовать оператор for. |
| 26 | Для функции $F = -\frac{2X}{(X^2\ -\ 1)^2\ +\ 1}$ и вводимого значения $X$ при $K$ приращениях аргумента $DX = (0.1;\ -0.05;\ 0.025;\ -0.0125;\ …)$ вычислить:
Результаты вычислений и соответствующие значения $DX$ вывести в виде таблицы с заголовками столбцов. Для организации цикла использовать оператор while. |
| 27 | Для функции $F = \cos(X)\ -\ \frac{1}{\cos^2(X)}$ и вводимого значения $X$ при $K$ приращениях аргумента $DX = (0.08;\ 0.04;\ 0.02;\ …)$ вычислить:
Результаты вычислений и соответствующие значения $DX$ вывести в виде таблицы с заголовками столбцов. Для организации цикла использовать оператор for. |
| 28 | Для функции $F = \frac{-1}{(X\ -\ 1)^2 \sqrt{1\ -\ (\frac{1}{X\ -\ 1})^2}}$ при $X = 10$ и $12$ приращениях аргумента $DX = (\frac{1}{4},\ \frac{1}{6},\ \frac{1}{8},\ …)$ вычислить:
Результаты вычислений и соответствующие значения $DX$ вывести в виде таблицы с заголовками столбцов. Для организации цикла использовать оператор for. |
| 29 | Для функции $F = \frac{X}{\sqrt{X^2\ +\ 1}}$ при $X = 0.95$ и приращениях аргумента $DX = (0.0005;\ 0.001;\ 0.002;\ 0.04;\ 0.08;\ 0.016;\ 0.032)$ вычислить в цикле do-while:
Результаты вычислений и соответствующие значения $DX$ вывести в виде таблицы с заголовками столбцов. |
| 30 | Упростив вычисления за счет использования дополнительных переменных и/или скобочных форм, вычислить значения функции $Y = \frac{a^{X^2\ -\ 1}\ +\ a^{X\ -\ 1}}{X\ -\ 1}$ и ее производной $Y'(X) = \frac{(2Xa^{X^2\ -\ 1}\ +\ a^{X\ -\ 1}) \ln(a) (X\ -\ 1)\ -\ (a^{X^2\ -\ 1}\ +\ a^{X\ -\ 1})}{(X\ -\ 1)^2}$ на $20$-ти значениях $X = (\frac{1}{2},\ \frac{3}{4},\ \frac{7}{8},\ …,\ \frac{2^{20}\ -\ 1}{2^{20}})$. Для проверки правильности вычислений $Y’$ вычислить также ее значение по заданной формуле без преобразований. Вычисленные значения вывести с предшествующими порядковыми номерами и соответствующими значениями аргумента $X$ в виде таблицы с заголовками столбцов. Для организации цикла использовать оператор for. |
Образец выполнения (вариант №6)
Условие задачи
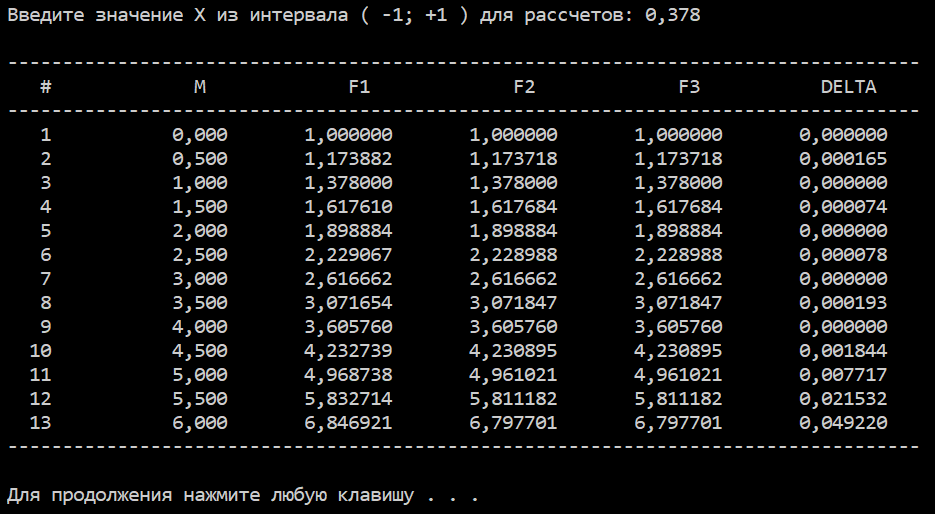
Вычислить при $M$, изменяющемся от $0$ до $6$ с шагом $0.5$, и вывести в виде таблицы с заголовками:
Для организации цикла использовать оператор while. При вычислениях приближенных значений использовать только операции сложения, вычитания, умножения, деления. |
Реализация задачи на языке С
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 | #include <stdio.h> // для консольного ввода-вывода #include <stdlib.h> // для задержки программы #include <locale.h> // русификация диалогов #include <math.h> // для математической функции pow - возведение в степень // параметр М меняется от 0 до 6 с шагом 0.5 #define M_LEFT 0.0 #define M_RIGHT 6.0 #define STEP 0.5 // заданная функция double F( const double X, const double M ) { return pow( 1.0 + X, M ); } // главная функция программы (точка входа) int main( void ) { // значение аргумента заданной функции double X; // отвечает за значение функции, вычисляемой по прямой формуле double f1; // отвечает за значение функции, вычисляемой приближенно, через вспомогательные переменные double f2; // отвечает за значение функции, вычисляемой приближенно, без вспомогательных переменных double f3; // список дополнительных переменных double a, b, c, d; // счетчик итераций вычислений size_t iter = 0; double M = M_LEFT; setlocale( LC_ALL, "Russian" ); printf( "Введите значение Х из интервала ( -1; +1 ) для рассчетов: " ); scanf_s( "%lf", &X ); // печатаем шапку таблицы printf( "\n-----------------------------------------------------------------------------------" ); printf( "\n # M F1 F2 F3 DELTA" ); printf( "\n-----------------------------------------------------------------------------------" ); while( M < ( M_RIGHT + STEP / 4 ) ) { iter++; // вычисляем значение функции по прямой формуле f1 = F( X, M ); // вычисляем значение функции через вспомогательные переменные a = M * X; b = a * ( M - 1 ) * X * 1.0 / 2.0; c = b * ( M - 2 ) * X * 1.0 / 3.0; d = c * ( M - 3 ) * X * 1.0 / 4.0; f2 = 1.0 + a + b + c + d; // вычисляем значение функции без вспомогательных переменных f3 = 1.0 + M * X + M * ( M - 1 ) * X * X / 2.0 + M * ( M - 1 ) * ( M - 2 ) * X * X * X / 6.0 + M * ( M - 1 ) * ( M - 2 ) * ( M - 3 ) * X * X * X * X / 24.0; // выводим строку результатов вычисления на экран printf( "\n%4u %15.3lf%15.6lf%15.6lf%15.6lf%15.6lf", iter, M, f1, f2, f3, fabs( f3 - f1) ); // значение параметра М меняется на величину 0.5 M += STEP; } printf( "\n-----------------------------------------------------------------------------------" ); // задержка работы программы, чтобы у пользователя была возможность просмотреть результат printf( "\n\n" ); system( "pause" ); return EXIT_SUCCESS; } |
Результаты работы программы
| ВНИМАНИЕ | Для получения программы своего варианта пишите на наш электронный адрес proglabs@mail.ru |
Варианты задания №2
💡 Во всех заданиях использовать только простые циклы
| № | Условие |
| 10 | В массиве $M$$(5)$ хранятся в порядке возрастания значения $1,\ 5,\ 10,\ 50,\ 100$. Требуется найти для положительного целого числа $N$ и сохранить в массиве $K$$(5)$ коэффициенты разложения $N = K_1 \cdot M_1\ +\ K_2 \cdot M_2\ +\ K_3 \cdot M_3\ +\ K_4 \cdot M_4\ +\ K_5 \cdot M_5$, при которых сумма $\sum\limits_{i = 1}^5 K_i$ будет минимальна (использовать операции $<\%>, </>)$. |
| 11 | В целочисленном массиве $M$$(N)$, $N \leq 20$, содержатся разные числа от $1$ до $k$, $k \lt N$, а в массиве $S$$(k)$ — не повторяющиеся числа от $1$ до $k$ в произвольном порядке. Требуется зашифровать данные массива $M$ следующим образом: новым значением элемента массива $M$ будет значение элемента массива $S$, индекс которого равен значению этого элемента массива $M$. Затем расшифровать $i$-ое значение массива $M$ и присвоить результат переменной $P$. |
| 12 | Выполнить циклический сдвиг элементов массива $X$$(N)$, $N \leq 10$, в результате которого значение последнего элемента должно оказаться на месте первого, а остальные — сдвинутыми на одну позицию в сторону увеличения индекса. |
| 13 | На заданном отрезке, с заданным шагом изменения аргумента вычислить и поместить в массив $F$ $30$ значений функций $e^{-x} \sin(6x)$, деленные на ее последнее положительное значение. |
| 14 | $S$ является последовательностью нулей и единиц длиной $L \leq 30$. Требуется сохранить в массиве $Y$ информацию, представленную $S$, в виде: $Y_0 = S_1$, а далее — числа, представляющие длины локальных подпоследовательностей с одинаковыми значениями. Подсчитать количество записанных в массив $Y$ чисел. |
| 15 | Восстановить последовательность $S$ (см. предыдущий пункт задания) по данным из массива $Y$ и количеству записанных в массив $Y$ чисел. |
| 16 | Последовательность $S$ из нулей и единиц длиной $L \leq 30$ зашифровать и поместить в массив $D$. Шифровать по следующему правилу: положить $D_1 = S_1$, а далее $D_i = 1$, если $S_i = S_{i\ -\ 1}$, иначе — $0$. Затем по данным из $D$ расшифровать последовательность и поместить в массив $R$. |
| 17 | В массиве $X$$(4)$ хранятся в порядке возрастания значений положительные вещественные числа. Требуется найти и сохранить в целочисленном массиве $K$$(4)$ коэффициенты разложения переменной $R$: $R = D\ +\ K_0 \cdot X_0\ +\ K_1 \cdot X_1\ +\ K_2 \cdot X_2\ +\ K_3 \cdot X_3$, где $D \lt X_0$, при котором сумма $\sum\limits_{i = 1}^4 k_i$ будет минимальна. |
| 18 | Из массива $X$$(N)$, $N \leq 20$, упорядоченного по невозрастанию значений элементов, переписать в массив $Y$ без повторов значения элементов с четными индексами, меньшие $C$, сохранив упорядоченность. |
| 19 | Изменяя $X$ от заданного начального значения с заданным шагом $H$ вычислить и поместить в массив $F$ $20$ значений разности функции $e^{-X} \sin(6X)$ и ее значением в точке первого локального минимума. |
| 20 | В массиве $V$$(10)$, заданном начальными значениями, содержатся разные числа от $0$ до $9$ в произвольном порядке. Требуется поместить в массив $D$ зашифрованную произвольную последовательность $S$ длины $L \leq 30$ из целых чисел от $0$ до $9$. Шифрование выполнить по следующему правилу: $D_i = i — V_{S_i}$. Затем по данным из $D$ расшифровать $k$-тую цифру и поместить в $R$. |
| 21 | Найти и сохранить в массиве $N$ коэффициенты $n_0,\ n_1,\ n_2,\ n_3,\ n_4,\ n_5$ разложение целого числа $K$$ (0 \lt K \lt 10^6)$ по степеням числа $10$. |
| 22 | Выполнить циклический сдвиг элементов массива $X$$(N)$, $N \leq 20$, на $K$ позиций, в результате которого последние $K$ элементов займут место в начале массива, а остальные будут сдвинуты на $K$ позиций в сторону увеличения индекса. Использовать дополнительный массив $D$. |
| 23 | На заданном отрезке, с заданным шагом изменения аргумента вычислить и поместить в массив $X$$(20)$ значения аргумента функции $e^{-x} \sin(3x)\ -\ 0.2$, предшествующие изменению знака функции, и подсчитать их количество. Вычисления производить либо до достижения границы интервала, либо до заполнения массива. |
| 24 | В массив $X$$(N)$, $N \leq 20$, упорядоченный по возрастанию значений элементов, добавить новое число так, чтобы не нарушать упорядоченность. |
| 25 | $S$ является последовательностью из чисел $1,\ 2,\ 3$ и $4$ длины $L \leq 20$. Требуется сохранить в массивах $K$ и $N$ информацию, представленную $S$, в виде: $K_i$ — число из $i$-той подпоследовательности из одинаковых чисел в $S$, $N_i$ — длина этой подпоследовательности, а также количество записанных в массивы $K$ и $N$ чисел. |
| 26 | Из массива $X$, упорядоченного по невозрастанию значений элементов, переписать в массив $Y$ числа, исключив их повторы и обеспечив упорядоченность по возрастанию. |
| 27 | Поместить положительные элементы массива $X$ в начало массива $Y$, а следом — его отрицательные элементы. |
| 28 | Из целочичсленного массива $X$$(N)$, $N \leq 20$, удалить числа, кратные $K$, поместив остальные числа в его начале без пропусков, не изменив их взаимного расположения. Вывести количество оставленных в массиве чисел и эти числа. |
| 29 | Найти и сохранить в массиве $K$$(N)$, $N \leq 14$, старшие $N$ цифр правильной дроби $R$ при представлении ее в десятичной системе счисления, а в переменной $D$ — часть числа $R$, меньшую $10^{-N}$. Использовать стандартные функции floor и ceil. |
| 30 | На заданном отрезке, с заданным шагом измерения аргумента вычислить и поместить в массив $X$$(50)$ значения аргумента функции $e^{-3x} \sin^2(20x)$, предшествующие первому локальному экстремуму функции типа максимум, а в массив $Y$ — соответствющие значения функции. Если за $50$ шагов экстремум не будет найден, то вывести соответствующее сообщение, иначе вывести помещенные в массивы $X$ и $Y$ значения в виде таблицы. |
| 31 | Из массива $X$$(20)$, упорядоченного по неубыванию значений элементов, переписать в массив $Y$ числа, исключив их повторы и добавив новое вводимое значение $P$ так, чтобы не нарушить упорядоченность. |
| 32 | На заданном отрезке, с заданным шагом изменения аргумента вычислить и поместить в массив $X$$(12)$ значения аргумента функции $e^{-\frac{x}{3}} \sin^2(5x)$, непосредственно предшествующие локальным максимальным приращениям функции. Если до достижения верхней границы интервала массив окажется заполненным, то вычисления прекратить и сопроводить вывод результатов соответствующим сообщением. |
| 33 | Поместить элементы массива $X$ в начало массива $Y$ в обратном порядке, исключив элементы, превосходящие по абсолютной величине вводимое значение $R$. |
| 34 | В массиве $K$ с индексами от $0$ до $9$, заданном начальными значениями, содержатся разные числа от $0$ до $9$ в произвольном порядке. Требуется поместить в массив $Y$ зашифрованную произвольную последовательность $X$ длины $L \leq 30$ из целых чисел от $0$ до $9$. Шифрование выполнить по следующему правилу: $Y_i = i — K_{X_i}$. Затем по данным из $Y$ расшифровать последовательность и поместить в массив $P$. Использовать дополнительный массив $T$ с начальными значениями, заданными следующим образом: $T_i$ равно номеру ячейки массива $K$ со значением $i$. |
Образец выполнения (вариант №21)
Условие задачи
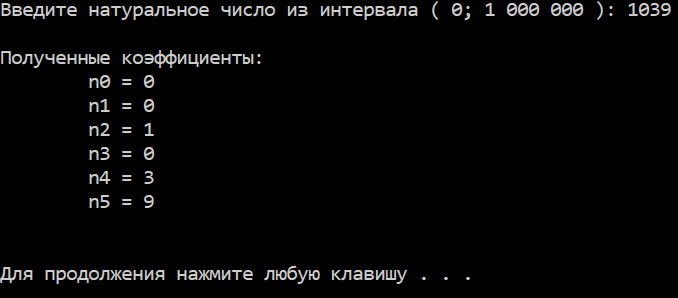
Найти и сохранить в массиве $N$ коэффициенты $n_0,\ n_1,\ n_2,\ n_3,\ n_4,\ n_5$ разложение целого числа $K$$ (0 \lt K \lt 10^6)$ по степеням числа $10$.
Алгоритм решения
Для успешного решения нужно понимать, что такое развернутая форма числа.
Развернутая форма записи числа — запись заданного числа в виде суммы произведений его цифр на основание системы счисления в соответствующей номеру позиции степени.
В нашем примере основание степени равно $10$. Рассмотрим конкретный пример. Допустим, дано число $78$. Запишем развернутую форму записи этого числа:
$78 = 7 \cdot 10^1\ +\ 8 \cdot 10^0$.
Рассмотрим другой пример. Допустим, дано число $1039$. Запишем разернутую форму записи этого числа:
$1039 = 1 \cdot 10^3\ +\ 0 \cdot 10^2\ +\ 3 \cdot 10^1\ +\ 9 \cdot 10^0$.
Т к по условию задачи требуется получить $6$ коэффициентов $\{n_0,\ n_1,\ n_2,\ n_3,\ n_4,\ n_5\}$, то числа можно «дополнять» ведущими нулями, например: $1534 \rightarrow 001534$.
$000078 = 0 \cdot 10^5\ +\ 0 \cdot 10^4\ +\ 0 \cdot 10^3\ +\ 0 \cdot 10^2\ +\ 7 \cdot 10^1\ +\ 8 \cdot 10^0$.
$\{n_0,\ n_1,\ n_2,\ n_3,\ n_4,\ n_5\} = \{0,\ 0,\ 0,\ 0,\ 7,\ 8 \}$
$001039 = 0 \cdot 10^5\ +\ 0 \cdot 10^4\ +\ 1 \cdot 10^3\ +\ 0 \cdot 10^2\ +\ 3 \cdot 10^1\ +\ 9 \cdot 10^0$.
$\{n_0,\ n_1,\ n_2,\ n_3,\ n_4,\ n_5\} = \{0,\ 0,\ 1,\ 0,\ 3,\ 9 \}$
💡 Следовательно, цель данной задачи — разбить входное число (с учетом ведущих нулей) на отдельные цифры, сохранив их в нужные элементы массива $N$. Так как требуется получить $6$ коэффициентов, то можно использовать цикл со счетчиком for.
Реализация задачи на языке С
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | #include <stdio.h> // для ввода-вывода #include <stdlib.h> // задержка программы #include <locale.h> // русификация диалогов // главная функция программы (точка входа) int main( void ) { #define SIZE 6 unsigned int N[ SIZE ]; int i; unsigned int K; setlocale( LC_ALL, "Russian" ); printf( "Введите натуральное число из интервала ( 0; 1 000 000 ): "); scanf( "%u", &K ); // получаем все цифра заданного числа, начиная с самого правого for( i = SIZE - 1; i >= 0; i-- ) { N[ i ] = K % 10; K /= 10; } printf( "\nПолученные коэффициенты:\n" ); for( i = 0; i < SIZE; i++ ) { printf( "\tn%d = %u\n", i, N[ i ] ); } // задержка программы, чтобы у пользователя была возможность просмотреть результат printf( "\n\n" ); system( "pause" ); return EXIT_SUCCESS; } |
Результаты работы программы
| ВНИМАНИЕ | Для получения программы своего варианта пишите на наш электронный адрес proglabs@mail.ru |
Варианты задания А
| № | Условие |
| 1 | Вычислить среднее геометрическое и наименьшее значение среди положительных элементов, сумму и наибольшее значение среди отрицательных элементов в массиве $D$$(N)$, $N \leq 25$. Вывести массив, среднее геометрическое, сумму, наименьшее и наибольшее значения. |
| 2 | Найти наибольшее и наименьшее значения, их индексы и среднее арифметическое отрицательных элементов, расположенных между ними, в массиве $D$$(n)$, $n \leq 25$. Вывести массив, среднее арифметическое, наименьшее и наибольшее значения и их индексы. |
| 3 | Найти наибольшее и наименьшее значения, их индексы и среднее геометрическое положительных, расположенных между ними, в массиве $D$$(n)$, $n \leq 25$. Вывести массив, наименьшее и наибольшее значения, их индексы, среднее геометрическое. |
| 4 | Вычислить среднее арифметическое значение элементов, удовлетворяющих условию $a \lt D_i \lt b$, найти наибольшее значение среди отрицательных элементов и его индекс в массиве $D$$(n)$, $n \leq 25$. Вывести массив, среднее арифметическое, наибольшее значение и его индекс. |
| 5 | Вычислить среднее арифметическое элементов массива $D$$(n)$, $n \leq 25$, а также найти элемент, отличающийся от среднего на наибольшую величину. Вывести массив, среднее, и найденный элемент. |
| 6 | Вычислить среднее арифметическое элементов массива $D$$(n)$, $n \leq 25$, без учета максимального и минимального элементов. Вывести массив, среднее, наибольший и наименьший элементы. |
| 7 | Из массива $D$$(n)$, $n \leq 25$ переписать элементы, расположенные между средним геометрическим и средним арифметическим модулей элементов, подряд в массив $F$. Вывести массивы, среднее арифметическое и среднее геометрическое. |
| 8 | Вычислить среднее геометрическое положительных элементов, кратных заданному числу, и сумму отрицательных элементов, кратных другому заданному числу, в массиве $D$$(n)$, $n \leq 25$. Вывести массив, среднее геометрическое и сумму. |
| 9 | Найти наибольший положительный элемент среди элементов с четными индексами, и сумму элементов с нечетными индексами, больших найденного наибольшего, в массиве $D$$(n)$, $n \leq 25$. Вывести массив, наибольший элемент и сумму. |
| 10 | Вычислить количество четных и нечетных элементов массива $D$$(n)$, $n \leq 25$. Если число четных элементов больше, то вычислить среднее арифметическое всех элементов массива, в противном случае — среднее геометрическое положительных. Вывести массив, количество четных и нечетных чисел, среднее арифметическое или среднее геометрическое. |
| 11 | Найти наибольшее и наименьшее значения и их индексы в массиве $D$$(n)$, $n \leq 25$. Наименьший элемент заменить суммой предшествующих элементов, а наибольший — произведением последующих. Вывести массив, наименьшее, наибольшее значения, их индексы, сумму и произведение. |
| 12 | Найти наибольшее и наименьшее значения и их индексы в массиве $D$$(n)$, $n \leq 25$. Вычислить их среднее значение и переписать в массив $B$ без пропусков элементы, расположенные в $\sigma$ окрестности найденного среднего. Вывести массивы $D$ и $B$, наименьшее, наибольшее значения, их индексы, среднее. |
| 13 | Определить в массиве $D$$(n)$, $n \leq 25$ элемент, который при умножении на последующий дает максимальное произведение. Для последнего элемента последующим считать первый. Вывести массив, найденный элемент и наибольшее произведение. |
| 14 | В массиве $X$$(n)$, $n \leq 25$ вычислить среднее арифметическое элементов, расположенных в интервале $[A,\ B]$, и среднее арифметическое элементов, лежащих вне этого интервала. Вычислить произведение элементов, расположенных между найденными средними. Вывести массив, произведение, средние значения. |
| 15 | В массиве $X$$(n)$, $n \leq 25$ найти первый и последний положительные элементы. Найти сумму элементов, расположенных между найденными элементами и произведение элементов, лежащих вне этого интервала. Вывести массив, найденные элементы, сумму и произведение. |
| 16 | Вычислить отношение $C = \frac{A}{B}$, где $A$ — сумма элементов, больших полусуммы наименьшего и наибольшего элементов массива $D$$(n)$, $n \leq 25$, а $B$ — сумма элементов по абсолютному значению меньших найденной полусуммы. Вывести массив, наибольший, наименьший элементы, суммы и их отношение. |
| 17 | Определить в массиве $D$$(n)$, $n \leq 25$ элемент, который при сложении с последующим дает максимальную сумму. Для последнего элемента последующим считать первый. Вывести массив, найденный элемент и наибольшую сумму. |
| 18 | В массиве $X$$(n)$, $n \leq 25$, все элементы которого расположены по неубыванию, найти среднее арифметическое всех элементов. Найти в массиве элемент, замена которого средним арифметическим не нарушит упорядоченность, и провести замену. Вывести массив, найденное среднее. |
| 19 | В массиве $D$$(n)$, $n \leq 25$, вычислить полусумму наибольшего и наименьшего элементов. Переписать в массив $C$ сначала элементы, не большие полусуммы, а затем — большие. Вычислить отношение $R = \frac{A}{B}$, где $A$ — сумма по абсолютной величине элементов первой части массива $C$, а $B$ — сумма элементов второй части массива $C$. |
| 20 | В массиве $D$$(n)$, $n \leq 25$ найти наибольшее четное и наибольшее нечетное числа. Переписать в массив $C$ все числа, расположенные вне интервала между найденными наибольшими. Вычислить среднее арифметическое элементов массива $C$. Вывести массив, наибольшие, среднее арифметическое. |
| 21 | Найти наибольшее и наименьшее значения и их индексы в массиве $D$$(n)$, $n \leq 25$. Если индекс наименьшего значения меньше индекса наибольшего, то вычислить сумму элементов, стоящих после наименьшего, в противном случае произведение элементов, стоящих после наибольшего. Вывести массив, наименьшее и наибольшее значения и их индексы, сумму или произведение. |
| 22 | Вычислить среднее геометрическое элементов до первого отрицательного и среднее арифметическое до первого положительного элемента в массиве $D$$(n)$, $n \leq 25$. Вывести массив, среднее геометрическое и среднее арифметическое. |
| 23 | Вычислить среднее арифметическое элементов массива $X$$(n)$, $n \leq 25$. Подсчитать количество элементов, лежащих в окрестности найденного среднего, найти среди этих элементов наибольший и наименьший. Вывести массив, среднее, количество, наибольший и наименьший элементы. |
| 24 | Найти наименьший положительный и наибольший отрицательный элементы массива $D$$(n)$, $n \leq 25$. Переписать в массив $C$ элементы, расположенные в интервале между найденными элементами и вычислить их среднее арифметическое. Вывести массив, наименьшее и наибольшее значения, среднее. |
| 25 | Подсчитать в массиве $X$$(n)$, $n \leq 25$ количество отрицательных и положительных элементов. Если отрицательных больше, то вычислить их среднее арифметическое, иначе — среднее геометрическое положительных. Вывести массив, количество положительных и отрицательных, среднее арифметическое или среднее геометрическое. |
| 26 | Найти наибольшее и наименьшее значения и их индексы в массиве $D$$(n)$, $n \leq 25$. Наименьший элемент заменить суммой отрицательных элементов, а наибольший — произведением положительных. Вывести массив, наименьшее, наибольшее значения, их индексы, сумму и произведение. |
Образец выполнения (вариант №15)
Условие задачи
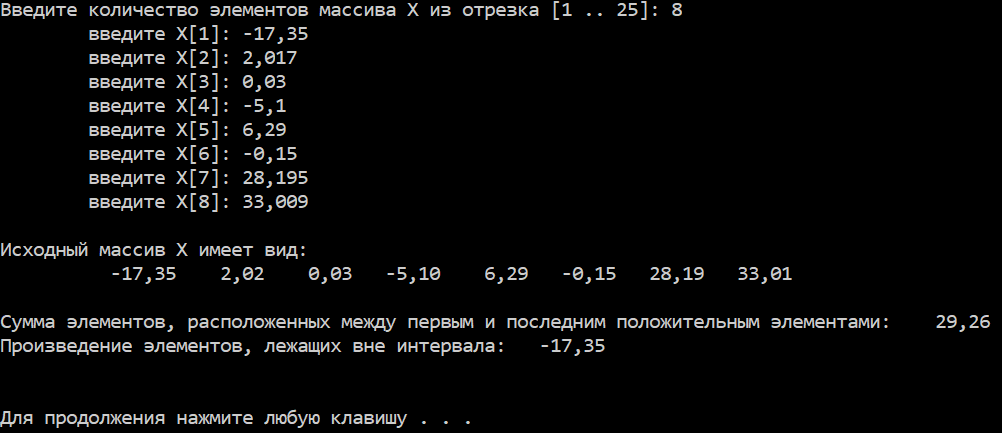
В массиве $X$$(n)$, $n \leq 25$ найти первый и последний положительные элементы. Найти сумму элементов, расположенных между найденными элементами и произведение элементов, лежащих вне этого интервала. Вывести массив, найденные элементы, сумму и произведение.
Реализация задачи на языке С
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 | #include <stdio.h> #include <locale.h> #include <stdlib.h> int main( void ) { // максимальное количество элементов массива X #define MAX 25 float X[ MAX ]; float p; int N, i; // индексы первого и последнего среди положительных элементов массива int index_first, index_last; setlocale( LC_ALL, "Russian" ); // запрос от пользователя количества элементов массива Х printf( "Введите количество элементов массива Х из отрезка [1 .. %d]: ", MAX ); scanf( "%d", &N ); // заполнение элементов массива вещественными числами вводом с клавиатуры for( i = 0; i < N; i++ ) { printf( "\tвведите X[%d]: ", i + 1 ); scanf( "%f", &X[ i ] ); } // вывод на экран текущего значения элементов массива Х printf( "\nИсходный массив Х имеет вид:\n\t" ); for( i = 0; i < N; i++ ) { printf( "%8.2f", X[ i ] ); } // находим индекс первого положительного элемента index_first = -1; for( i = 0; i < N; i++ ) { if( X[ i ] > 0 ) { index_first = i; break; } } // находим индекс последнего положительного элемента index_last = -1; for( i = N - 1; i >= 0; i-- ) { if( X[ i ] > 0 ) { index_last = i; break; } } if( index_first == - 1) { printf( "\n\nЗаданный массив Х не содержит ни одного положительного элемента! Нахождение суммы невозможно.\n" ); } else { // находим сумму элементов, расположенных между index_first и index_last float sum = 0.0; for( i = index_first + 1; i <= index_last - 1; i++ ) { sum += X[ i ]; } printf( "\n\nСумма элементов, расположенных между первым и последним положительным элементами: %8.2f\n", sum ); } // находим произведение элементов, лежащих вне интервала if( ( index_first == 0 ) && ( index_last == N - 1 ) ) { printf( "Нет ни одного элемента, попадающего вне найденного интервала! Нахождение произведения невозможно.\n" ); } else { p = 1.0; for( i = 0; i < index_first; i++ ) { p *= X[ i ]; } for( i = index_last + 1; i < N; i++ ) { p *= X[ i ]; } printf( "Произведение элементов, лежащих вне интервала: %8.2f\n", p ); } // задержка работы программы, чтобы у пользователя была возможность просмотреть результат printf( "\n\n" ); system( "pause" ); return EXIT_SUCCESS; } |
Результаты работы программы
Варианты задания B
Во всех заданиях не использовать аналитических формул производных заданных функций. Ввод исходных данных выполнить с применением переменных $X_{нач},\ X_{кон},\ h_x$. Найденные значения выводить с поясняющими текстами.
| № | Условие |
| 1 | Составить программу вычисления максимального и минимального значения функции $Y = 3X^3\ -\ 15X^2\ -\ 12X\ +\ 8$ и соответствующих значений аргумента при его изменении на интервале от $-5$ до $15$ с шагом $0.01$. |
| 2 | Составить программу нахождения локальных минимумов функции $X^2 \cdot \sin^3(3X)$ при изменении аргумента от $-3$ до $2.5$ с шагом $0.001$. Среди найденных минимумов найти точку с наибольшим значением функции. |
| 3 | Составить программу вычисления локальных максимумов функции $X^3 \cdot \sin^5(4X)$ при изменении аргумента на интервале от $-1.6$ до $3.2$ с шагом $0.001$. Среди найденных максимумов найти точку с наименьшим значением функции. |
| 4 | Составить программу вычисления минимального расстояния между точками экстремумов-минимумов функции $(1\ +\ 6sin^2(X))^{\frac{1}{2}} \cdot \cos(3X)$ и соответствующих значений функции при изменении $X$ на интервале $-5$ до $12$ с шагом $0.001$. |
| 5 | Произвольные значения аргумента функции $Y = 2X^4\ -\ 12X^3\ -\ 4X^2\ +\ 2$ находятся в массиве $X$$(n)$, $n \leq 20$. Составить программу вычисления максимального и минимального значений функции, а также соответствующих значений элементов массива $X$ и их индексов. |
| 6 | Известно, что в интервале $-7$ до $7$ уравнение $\cos(2.5X) \cdot \sin(3X)\ -\ 0.2 = 0$ имеет несколько корней. Составить программму нахождения корней уравнения, а также корня, в котором производная функции имеет максимальное значение. |
| 7 | Известно, что в интервале $-10$ до $20$ функция $Y = 4^{-(x\ -\ 1)^2} \cos(2X)$ имеет несколько точек перегиба. Составить программу нахождения точек перегиба, а также той из них, где первая производная функции имеет максимальное значение. |
| 8 | Составить программу вычисления минимального расстояния между точками локальных максимумов функции $(X\ +\ 1) \sin(1.5X)\ +\ X \cos(1.5X)$ при изменении $X$ на интервале $-3.2$ до $8$ с шагом $0.001$. |
| 9 | Известно, что в интервале $-7$ до $7$ уравнение $\sin(2.5X) \cos(3X)\ +\ 0.2 = 0$ имеет несколько корней. Составить программу нахождения корней уравнения, а также корня, в котором производная функции имеет минимальное значение. |
| 10 | Найти на кривой $Y$$(X) = \sin^3(3X) \cos(2X)$ все точки, принадлежащие интервалу $[a,\ b]$ и расположенные на минимальном расстоянии от прямой $Y = 2$. |
| 11 | В массивах $X$$(N)$, $Y$$(N)$, $N \leq 20$, заданы координаты точек на плоскости. Найти такие точки, для которых расстояние $d = |\frac{aX_i\ +\ bY_i\ +\ c}{\sqrt{a^2\ +\ b^2}}|$ от точки $(X_i,\ Y_i)$ до прямой $aX\ +\ bY\ +\ c$ находится в интервале $[r_1,\ r_2]$. Среди найденных точек найти наименее и наиболее удаленные от плоскости. |
| 12 | Найти на кривой $Y$$(X) = \sin^2(2X) \cos(4X)$ точку, абсцисса которой принадлежит интервалу $[r_1,\ r_2]$ и сумма расстояний от которой до прямых $a_1x\ +\ b_1y\ +\ c_1 = 0$ и $a_2x\ +\ b_2y\ +\ c_2 = 0$ минимальна. |
| 13 | Составить программу вычисления значения аргумента, изменяя его на интервале от $-4$ до $10$ с шагом $0.001$, при котором производная функции $Y = X^2 \sin^2(X) \cos(3X)$ имеет минимальное и максимальное значение. |
| 14 | В массиве $X$$(N)$, $N \leq 30$, заданы абциссы точек, принадлежащих кривой $Y = X^2 \sin(2X) \cos(3X)$. Среди этих точек найти точки наиболее и наименее удаленные от прямой $ax\ +\ by\ +\ c = 0$. |
| 15 | Составить программу вычисления максимального расстояния между экстремумами-минимумами функции $Y = x(\sin(3X)\ +\ \cos(2x))$ и соответствующих значений функции при изменении $X$ на интервале $-3.5$ до $4.5$ с шагом $0.001$. |
| 16 | Составить программу нахождения локальных максимумов функции $X^2(\sin^3(3X)\ -\ \cos^2(2X))$ при изменении аргумента от $-3.5$ до $5.5$ с шагом $0.001$. Среди найденных максимумов найти точку с наименьшим значением производной. |
| 17 | Составить программу вычисления максимального расстояния между соседними корнями уравнения $2\cos(3X)\ -\ 3\sin(2X)\ +\ 0.1 = 0$, изменяя $X$ на интервале $-4$ до $3$ c шагом $0.001$. |
Добавить комментарий