Содержание
| ВНИМАНИЕ | Для получения программы своего варианта пишите на наш электронный адрес proglabs@mail.ru |
Задание А
Во всех задания $1-28$:
|
Варианты заданий
| № | Условие |
| 1 | $Z = X^2 \cdot Y^2 + 3 \cdot X \cdot Y^2\ -\ 5 \cdot X^2 \cdot Y + X^2\ -\ 2 \cdot Y^2 + 4 \cdot X \cdot Y\ -\ X + Y$ $X = (2;\ -2),\ Y = (4;\ -3)$ |
| 2 | $B = A + 2;\ C = \frac{A\ +\ 3}{A\ +\ 2};\ D = \frac{A\ +\ 4}{A\ +\ 3};\ E = \frac{A\ +\ 5}{A\ +\ 4}$ $A = (1;\ 2;\ -2;\ 3;\ 4)$ |
| 3 | $Z = (X + 2) \frac{(X\ +\ 2)^2 + 3}{(X\ +\ 2)^4 + (X\ +\ 2)^2 + 3}$, $X = (0;\ 1;\ 2;\ -2;\ 4)$ |
| 4 | $B = \sin(A);\ C = \log(A);\ D = e^A;\ E = |A|;$ $A = (8;\ -2;\ 4;\ -5)$ |
| 5 | $B = A + 5;\ C = A\ -\ 2;\ D = B + C;\ E = A\ -\ C;$ $A = (-15;\ -5;\ 0;\ 7;\ 14)$ |
| 6 | $B = A\ -\ 2;\ C = A + 3;\ D = B + C;\ E = A\ -\ 2;$ $A = (-4;\ 0;\ 4;\ 7)$ |
| 7 | $Y = \frac{3}{1\ +\ 3\ +\ X}\ -\ \frac{3\ \cdot\ 5}{1\ +\ 3\ +\ 5\ +\ 2\ \cdot\ X}\ +\ \frac{3\ \cdot\ 5\ \cdot\ 7}{1\ +\ 3\ +\ 5\ +\ 7\ +\ 3\ \cdot\ X}\ -\ \frac{3\ \cdot\ 5\ \cdot\ 7\ \cdot\ 9}{1\ +\ 3\ +\ 5\ +\ 7\ +\ 9\ +\ 4\ \cdot\ X}$ $X = (-9;\ -4;\ 0;\ 3;\ 9)$ |
| 8 | $Y = -X^6 + A \cdot X^5 — A^2 \cdot X^4 + A^3 \cdot X^3 — A^4 \cdot X^2 + A^5 \cdot X — A^6$ $X = (-3;\ 5),\ A = (-3;\ 5)$ |
| 9 | $Y = A^X\ -\ \frac{A^{2X}}{3}\ +\ \frac{A^{3X}\ \cdot\ 4}{3\ \cdot\ 5}\ -\ \frac{A^{4X}\ \cdot\ 6}{3\ \cdot\ 5\ \cdot\ 7}$ $X = (-3;\ 0;\ 3),\ A = 4$ |
| 10 | $Y = X\ +\ \frac{2\ \cdot\ 4\ \cdot\ X^2}{2\ +\ 4}\ +\ \frac{2\ \cdot\ 4\ \cdot\ 6\ \cdot\ X^3}{2\ +\ 4\ +\ 6}\ +\ \frac{2\ \cdot\ 4\ \cdot\ 6\ \cdot\ 8\ \cdot\ X^4}{2\ +\ 4\ +\ 6\ +\ 8}\ +\ \frac{2\ \cdot\ 4\ \cdot\ 6\ \cdot\ 8\ \cdot\ 10\ \cdot\ X^5}{2\ +\ 4\ +\ 6\ +\ 8\ +\ 10}$ $X = (-7;\ -2;\ 0;\ 2;\ 7)$ |
| 11 | $Y = (\frac{\sqrt[3]{A\ -\ B}\ \cdot\ (A\ +\ B)^{\frac{2}{3}}\ \cdot\ X^2}{A^4\ +\ B^4\ -\ 2\ \cdot\ A^2\ \cdot\ B^2\ -\ X^4})^{\frac{1}{X}}$ $X = (0.5;\ 1;\ 2),\ A = 4,\ B = 3$ |
| 12 | $Y = (\frac{A}{B})^X + (\frac{A}{B})^{2X} + 2(\frac{A}{B})^{-\frac{2}{3}} \cdot \log_2(\frac{A}{B})$ $X = (2.5;\ 5;\ 7;\ 10),\ A = 4,\ B = 3$ |
| 13 | $Y = \frac{-3.3\ \cdot\ 10^{-4}\ \cdot\ \tan(x)\ \cdot\ \log(X^2\ -\ 5)\ \cdot\ \sqrt{|\tan(X)|}}{\sqrt[3]{X^2\ -\ 5}\ \cdot\ X\ \cdot\ e^{-2X}}$ $X = (1;\ 2.5;\ 5;\ 7;\ 10)$ |
| 14 | $Y = \frac{\sqrt[3]{(X\ +\ 1)^2}\ \cdot\ (X\ +\ 2)\ \cdot\ ln(X\ +\ 1)}{(X\ +\ 2)^3\ -\ (X\ +\ 2)^2\ +\ (X\ +\ 1)^2}$ $X = (-0.5;\ 5;\ 10;\ 25)$ |
| 15 | $Y = \frac{\sqrt[3]{X^4\ +\ X^3\ -\ X^2\ -\ X\ +\ 1}}{X^4\ +\ 2X^3\ -\ 2X\ -\ 1} \qquad \qquad X = (-15;\ -5;\ -2;\ 2;\ 5)$ |
| 16 | $Y = \frac{X\ +\ X^3\ -\ 3}{2X^2\ -\ 4X\ +\ 2\ +\ 6X^3\ -\ 4X^5} \qquad \qquad X = (-5;\ -2;\ 2;\ 5)$ |
| 17 | $Y = \frac{\cos^4(X)}{4}\ -\ \frac{\cos^2(X)}{2} — \ln(|\cos(X)|)$ $X = (0^\circ;\ 30^\circ;\ 45^\circ;\ 60^\circ;\ 90^\circ)$ |
| 18 | $Y = (\frac{1}{2}\ +\ (X\ -\ 1)\ -\ \frac{(X\ -\ 1)^2}{2}\ +\ \frac{(X\ -\ 1)^4}{3}) / (X^2\ -\ 1)$ $X = (0;\ 1;\ 2;\ 3)$ |
| 19 | $Y = \frac{(\frac{1}{2}\ +\ \sin^2(X)\ \cdot\ \ln|\sin(X)|}{\frac{\pi}{3}\ -\ \arcsin(X)}\ \qquad X = (0.001;\ 0.1;\ 0.3;\ 0.5;\ 0.9;\ 1.8)$ |
| 20 | $Y = \frac{e^X\ -\ e^{2X}\ +\ e^{3X}\ \cdot\ \arccos^2(X)}{e^X\ -\ e^{2X}\ +\ e^{3X}\ \cdot\ \arcsin^{0.5}(X)}\ \qquad X = (0.001;\ 0.02;\ 0.1;\ 0.9)$ |
| 21 | $Y = \frac{| \frac{1}{4} — A^2\ \cdot\ \tan(X)|}{(\sin(X) + \cos(X))(\tan^2(X) + 1)} \qquad X = (0.001^\circ;\ 15^\circ;\ 30^\circ;\ 60^\circ;\ 270^\circ)$ |
| 22 | $Y = \frac{|\sin(X)\ \cdot\ \cos(X)|\ +\ \tan(X)}{\sin(X)\ +\ \sin(X)\ \cdot\ \cos(X)\ +\ \cos(X)}$ $X = (0.001^\circ;\ 15^\circ;\ 30^\circ;\ 60^\circ;\ 270^\circ)$ |
| 23 | $Y = \frac{2X^3\ +\ 6X^2\ -\ 8x\ +\ 4}{-4X^3\ +\ 8X^2\ -\ X^5\ +\ 2X^4} \qquad X = (-5;\ -2;\ 2;\ 5)$ |
| 24 | $Y = \frac{1\ -\ \sqrt{|log_2(X)|}\ +\ 25\ \cdot\ 10^{-5}\ \cdot \log_{10}(X)}{\log_2(X)\ +\ 0.00025\ \cdot\ \log_{10}(X)} \qquad X = (0.001;\ 0.1;\ -1;\ 1;\ 4)$ |
| 25 | $Y = \frac{X \lg(X\ +\ 1)\ +\ \lg(X\ +\ 1)\ +\ X \ln(A)\ +\ \ln(A)\ +\ A^{X\ +\ 1} \lg(X\ +\ 1)\ +\ A^{X\ +\ 1} \ln(A)}{\ln(A)\ +\ \ln(X\ +\ 1)}$ $X = (0.001;\ 0.1;\ -1;\ 1;\ 4),\ A = 3$ |
| 26 | $Y = \frac{A^X X^A\ +\ 2A^{2X} X^A\ -\ 2A^X X^{2A}\ -\ 4A^{2X} X^{2A}}{\log(A)\ +\ \log(X)}$ $X = (0.001;\ 0.1;\ 1;\ 4),\ A = 1.5$ |
| 27 | $Y = \frac{A^{X^A}\ \cdot\ X^{A^{A\ \cdot\ X}}}{A^{A\ \cdot\ X}\ +\ X^{A\ \cdot\ X}} \qquad \qquad X = (0.001;\ 0.1;\ 1;\ 4)$ и $A = 2$ |
| 28 | $Y = 1\ +\ \frac{X^2}{3^2}\ +\ \frac{X^2}{7^2}\ +\ \frac{X^2}{11^2}\ +\ \frac{X^4}{3^2 \cdot 7^2}\ +\ \frac{X^4}{3^2 \cdot 11^2}\ +\ \frac{X^4}{7^2 \cdot 11^2}\ +\ \frac{X^6}{3^2 \cdot 7^2 \cdot 11^2}$ $X = (-4;\ 0;\ 4;\ 11)$ |
| В заданиях $29$ и $30$ найти коэффициенты $k_0,\ k_1,\ k_2,\ …$ представления числа $X\ (0 \leq X \leq P^N)$ в позиционной системе счисления с основанием $P$, используя операции $/$ и $\%$. Для контроля результатов выполнить вычисление $X$ непосредственно по заданной формуле разложения $X$ по степеням $P$ для найденных коэффициентов, а также после преобразования выражения в формуле по схеме Горнера. Вывести все результаты вычислений в наглядной форме с поясняющими текстами. Проверить работу программы при вводимых значениях $X$ из набора $M$. |
| 29 | $P = 8,\ N = 4,\ X = k_4 \cdot 8^4\ +\ k_3 \cdot 8^3\ +\ k_2 \cdot 8^2\ +\ k_1 \cdot 8\ +\ k_0$ $M = \{0;\ 1;\ 2;\ 4;\ 7;\ 8;\ 65;\ 1023;\ 4095\}$ |
| 30 | $P = 16,\ N = 3,\ X = k_3 \cdot 16^3\ +\ k_2 \cdot 16^2\ +\ k_1 \cdot 16\ +\ k_0$ $M = \{0;\ 1;\ 15;\ 64;\ 127;\ 255;\ 2047;\ 4095\}$ |
| 31 | Найти среднее геометрическое абсолютных значений частных от целочисленного деления $X,\ X_2,\ X_3$ на $Y$ и среднее арифметическое остатков от целочисленного деления $X,\ X_2,\ X_3$ на $Y$. Для контроля результатов целочисленного деления выводить на экран с поясняющими надписями делимое, делитель, частное, абсолютное значение частного, остаток. Также с поясняющими текстами вывести найденные средние геометрические и средние арифметические. Проверить работу программы при вводе значений $X = (-5;\ 5)$ и $Y = (-3;\ 3)$. |
| 32 | Координаты вершины параллелепипеда заданы положительными значениями $X_1,\ X_2,\ Y_1,\ Y_2,\ Z_1,\ Z_2\ (X_1 < X_2,\ Y_1 < Y_2,\ Z_1 < Z_2)$, имеющими ненулевые дробные части. Требуется найти целочисленные координаты $I_1,\ I_2,\ J_1,\ J_2,\ K_1,\ K_2$ вершин такого параллелепипеда, который находится внутри заданного и имеет наибольший объем. Найти также объемы этих параллелепипедов и отношение объемов. Все значения $X_1,\ X_2,\ Y_1,\ Y_2,\ Z_1,\ Z_2$ и $I_1,\ I_2,\ J_1,\ J_2,\ K_1,\ K_2$ вывести на экран с поясняющими надписями, а найденные объемы и их отношения вывести с предшествующими поясняющими текстами. Проверить работу программы на вводимых $X_1 = (2.7;\ 5.2),\ X_2 = 2 \cdot X_1$ $Y_1 = X_1\ -\ 1;\ Y_2 = 2\ \cdot\ Y_1$ $Z_1 = \frac{X_1}{2},\ Z_2 = 3\ \cdot\ Z_1$. |
Задание Б
Во всех заданиях:
|
Варианты заданий
| № | Условие |
| 1 | Решить систему из двух линейных уравнений и проверить найденное решение подстановкой результатов в уравнение. |
| 2 | Вычислить площадь $S$ остроугольного треугольника, заданного координатами вершин на плоскости, по формуле Герона, а затем — величины углов, используя соотношение $\frac{L_a \ \cdot \ L_b \cdot \ \sin(C)}{2}$, где $C$ — угол между сторонами с длинами $L_a$ и $L_b$, а также, для проверки результатов, вычислить сумму углов. |
| 3 | Вычислить координаты точек на плоскости, делящих отрезок прямой, заданный координатами концов, в отношении $m : n : k$. Выполнить проверку работы программы вычислением $m$, $n$ и $k$ на основе полученных координат точек деления отрезка прямой. |
| 4 | Решить квадратное уравнение считая, что оно имеет только вещественные корни. Проверить результаты подстановкой корней в уравнение. |
| 5 | Вычислить коэффициенты уравнения прямой $Y = K \ \cdot \ X + B$, проходящей через точки с координатами $(X_1,\ Y_1)$ и $(X_2,\ Y_2)$, и найти точку пересечения этой прямой с осью абсцисс. Проверить результаты подстановкой в уравнение для заданных координат точек. |
| 6 | Вычислить координаты точки пересечения двух прямых, заданных уравнениями: $A \ \cdot \ X + B \ \cdot \ Y = C$ и $D \ \cdot X + E \ \cdot Y = F$. Проверить результаты подстановкой в уравнения. |
| 7 | Точка имеет координаты $X_0, \ Y_0$. Вычислить координаты точки после поворота осей координат относительно начала на угол $A$ против часовой стрелки. Проверить работу программы для: а) $A = arctg(\frac{Y_0}{X_0})$ |
| 8 | Вычислить координаты вершин треугольника, находящихся на пересечении прямых $Y = k_1 \cdot X + b_1$ и $Y = k_2 \cdot X + b_2$ между собой и с осью $X$. Найти площадь $S$ этого треугольника, а также длины сторон. Проверить работу программы вводом данных для уравнений $Y = X + 1$ и $Y = -X + 1$. |
| 9 | Вычислить координаты точек пересечения прямой ($A \cdot X + B \cdot Y = C$) и окружности ($X^2 + Y^2 = R^2$) на плоскости. Проверить результаты подстановкой в уравнения. |
| 10 | Вычислить площадь $S$ равнобедренного треугольника, вписанного в окружность радиуса $R$, если известна длина $L_a$ его стороны, не равная длинам других сторон. Найти также длины других сторон треугольника и угол $A$ между ними. Проверить работу программы на равностороннем треугольнике по его площади, которую следует вычислить заранее. |
| 11 | Вычислить координаты точки пересечения эллипса $A \cdot X^2 + B \cdot Y^2 = R^2$ и гиперболы $Y = \frac{C}{X}$. Проверить результаты при $A = B = C = 1,\ R^2 = 2$, должно быть $X_1 = X_3 = 1,\ Y_1 = Y_3 = 1,\ X_2 = X_4 = -1, Y_2 = Y_4 = -1$. |
| 12 | Найти числа $X$ и $Y$, произведение которых равно $A$, а разность равна $B$. Вывести найденные значения, а также, для контроля, — их произведение и разность. Проверить работу программы также при $A = 1,\ B = 0$, где решение очевидно. |
| 13 | Вычислить площадь треугольника, заданного координатами вершин в пространстве, по формуле Герона. Подобрать два варианта исходных данных для проверки работы программы. |
| 14 | Найти числа $X$ и $Y$, сумма которых равна $A$, а сумма квадратов равна $B$. Вывести найденные значения, а также, для контроля, — их сумму и сумму квадратов. Проверить работу программы также при вводе $A = 1,\ B = 1$, где решение очевидно. |
| 15 | Для треугольника, заданного длинами сторон $L_a,\ L_b,\ L_c$ найти угол, противоположный стороне длины $L_a$, используя соотношение $\sin(\frac{\alpha}{2} ) = \sqrt{\frac{(P\ -\ L_b) \cdot (P\ -\ L_c)}{L_b\ \cdot\ L_c}}$, где $P$ — полупериметр треугольника. Найти также другие углы. Проверить результаты для различных исходных данных по сумме углов. |
| 16 | Вычислить координаты точек пересечения кривых, заданных уравнениями $Y = X + C$ и $(\frac{X}{2})^2 + Y^2 = 1$. Проверить результаты подстановкой в исходные уравнения. |
| 17 | Вычислить площадь правильного $N$-угольника, вписанного в окружность радиуса $R$. Найти относительные ошибки замены площади круга площадью такого $N$-угольника при значениях $N$, равных $6,\ 60,\ 360$. Проверить правильность решения: при $N = 4$ и любом $R$ относительная ошибка должна быть равна $0.363$. |
| 18 | Вычислить площадь правильного $N$-угольника, в который вписана окружность диаметра $D$. Найти относительные ошибки замены площади такого $N$-угольника площадью круга при значениях $N$, равных $12,\ 120,\ 720$. Проверить правильность решения: при $N = 4$ и любом $D$ относительная ошибка должна быть равна $0.274$. |
| 19 | Вычислить площадь равнобедренного треугольника, вписанного в окружность радиуса $R$, если известен угол $A$ между его сторонами равной длины. Вычислить также отношение площади круга радиуса $R$ к площади треугольника. Проверить работу программы при вычислении отношения площади круга радиуса $R$ к площади треугольника при вводе следующих значений угла $A$:
|
| 20 | Найти числа $X$ и $Y$, сумма которых равна $A$, а разность $B$. Вывести найденные значения, а также, для контроля, — их сумму и разность. Проверить работу программы также при вводе $A = 1,\ B = 1$, где решение очевидно. |
| 21 | Для треугольника, заданного длинами сторон $L_a,\ L_b,\ L_c$, найти угол $\alpha$, противоположный стороне длины $L_a$, используя соотношение $\cos(\frac{\alpha}{2}) = \sqrt{\frac{P\ \cdot\ (P\ -\ L_a)}{L_b\ \cdot\ L_c}}$, где $P$ — полупериметр треугольника. Найти также другие углы. Проверить результаты для различных исходных данных по сумме углов. |
| 22 | На плоскости найти угол $A$ между двумя сторонами $(1,\ 2)$ и $(1,\ 3)$ остроугольного треугольника, заданного координатами вершин $X_1,\ Y_1,\ X_2,\ Y_2,\ X_3,\ Y_3\ (X_1 < X_2 < X_3)$, длины $L_{12},\ L_{13}$ этих сторон и затем — площадь треугольника $S$ по формуле $S = L_{12} \cdot L_{13} \cdot \frac{\sin(A)}{2}$. Значение угла $A$ вывести в градусах. Проверить работу программы при вводе $X_1 = 0,\ Y_1 = 0,\ X_2 = 1,\ Y_2 = 0,\ X_3 = 2,\ Y_3 = (2,\ -2)$. |
| 23 | Вычислить площадь $S$ равнобедренного треугольника, в который вписана окружность радиуса $R$, если известна длина $L_a$, его стороны не равная длинам других сторон. Найти также длину $L$ других сторон треугольника и его углы. Проверить работу программы на равностороннем треугольнике по его площади, которую следует вычислить заранее. |
| 24 | Найти площадь прямоугольного треугольника, в который вписана окружность радиуса $R$, а также значения углов, если известна длина $L_a$ его катета $K_a$. Для проверки работы программы предусмотреть вычисление $L_a$ по найденной длине $L_b$ другого катета. Проверить работу программы также при $R = 1,\ L_a = 2 + \sqrt 2$, когда прямоугольник будет равнобедренным. |
| 25 | Найти координаты центра тяжести треугольника на плоскости, то есть координаты точки, лежащей на медиане и отстоящей на $\frac{2}{3}$ ее длины от вершины, из которой медиана проведена. Для проверки результата выполнить вычисления для всех трех медиан. Проверить работу программы также для равнобедренного прямоугольного треугольника с координатами вершин $(0;\ 0),\ (3;\ 0),\ (0;\ 3)$, где решение очевидно. |
| 26 | Вычислить $S$ — площадь остроугольного треугольника по формуле $S = \frac{L_a\ \cdot\ L_b\ \cdot\ sin(C)}{2}$, где $L_a,\ L_b$ — длины сторон, а $C$ — угол между ними. Затем вычислить длину третьей стороны $L_c$, используя соотношение $L_c^2 = L_a^2 + L_b^2\ -\ 2 \cdot L_a \cdot L_b \cdot cos(C)$ и остальные углы, используя соотношение $\frac{sin(A)}{sin(C)} = \frac{L_a}{L_c}$. Проверить результаты для различных исходных данных по сумме углов. |
| 27 | Найти:
Проверить результаты, предварительно вычислив площадь треугольника с вершинами в этих точках при вводе $k_1 = 1,\ b_1 = 1,\ X_0 = 0,\ Y_0 = 2$. |
| 28 | Дано уравнение $A \cdot X^2 + B \cdot Y^2 + C \cdot X + D \cdot Y + E = 0$. Вычислить коэффициенты уравнения $A_1 \cdot X^2 + B_1 \cdot Y^2 + C_1 \cdot X + D_1 \cdot Y + E_1 = 0$, получающиеся после переноса начала координат в точку $X_1,\ Y_1$ и проверить результаты. Выполнить также проверку решения обратным преобразованием координат. |
Образец выполнения (вариант №4)
Условие задачи
Решить квадратное уравнение считая, что оно имеет только вещественные корни. Проверить результаты подстановкой корней в уравнение.
Реализация задачи на языке С
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 | #include <stdio.h> // для консольного ввода-вывода #include <locale.h> // для русификации диалогов программы #include <stdlib.h> // включает полезные функции и константы #include <math.h> // для использования мат.функций, например sqrt // главная функция программы (точка входа) int main( void ) { // коэффициенты квадратного уравнения double a, b, c; // отвечает за дискриминант double D; // корни уравнения double x1, x2; // русификация диалогов программы setlocale( LC_ALL, "Russian" ); // предлагаем пользователю ввести с клавиатуры коэффициенты квадратного уравнения #define EPS 0.00001 printf( "Введите коэффициент a( a <> 0 ): " ); scanf( "%lf", &a ); if( fabs( a ) <= EPS ) { printf( "Значение коэффициента а не может быть равно 0! Программа закрывается." ); printf( "\n\n" ); system( "pause" ); return EXIT_SUCCESS; } printf( "Введите коэффициент b: " ); scanf( "%lf", &b ); printf( "Введите коэффициент c: " ); scanf( "%lf", &c ); // находим дискриминант D = pow( b, 2 ) - 4 * a * c; // уравнение не имеет действительных корней ( D < 0 ) if( D < 0.0 ) { printf( "\nДискриминант ( D = %0.6lf ) меньше 0. \nКвадратное уравнение не имеет действительных корней.", D ); printf( "\n\n" ); system( "pause" ); return EXIT_SUCCESS; } // находим одинаковые корни ( D = 0 ) if( fabs( D ) <= EPS ) { x1 = x2 = (double)-b / ( 2 * a ); printf( "\nДискриминант ( D = %0.6lf ) равен 0. \nКвадратное уравнение имеет 2 одинаковых корня:\n", D ); printf( "\tX1 = X2 = %0.6lf\n", x1 ); } // находим 2 различных действительных корня ( D > 0 ) else { x1 = ( -b + sqrt( D ) ) / ( 2 * a ); x2 = ( -b - sqrt( D ) ) / ( 2 * a ); printf( "\nДискриминант ( D = %0.6lf ) больше 0. Квадратное уравнение имеет 2 различных корня:\n", D ); printf( "\tX1 = %10.6lf\n", x1 ); printf( "\tX2 = %10.6lf\n", x2 ); } // подставляем найденные значения в исходное квадратное уравнение { double y1 = a * pow( x1, 2 ) + b * x1 + c; double y2 = a * pow( x2, 2 ) + b * x2 + c; if( ( fabs( y1 ) <= EPS ) && ( fabs( y2 ) <= EPS ) ) printf( "\nНайденные значения X1 и X2 являются корнями заданного квадратного уравнения!" ); } // задержка работы программы, чтобы была возможность просмотреть результаты printf( "\n\n" ); system( "pause" ); return EXIT_SUCCESS; } |
Результаты работы программы

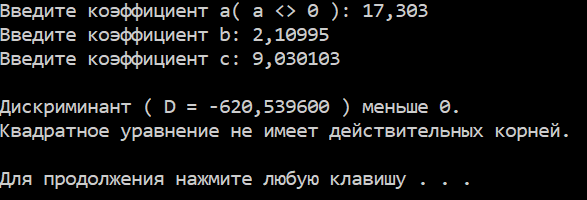
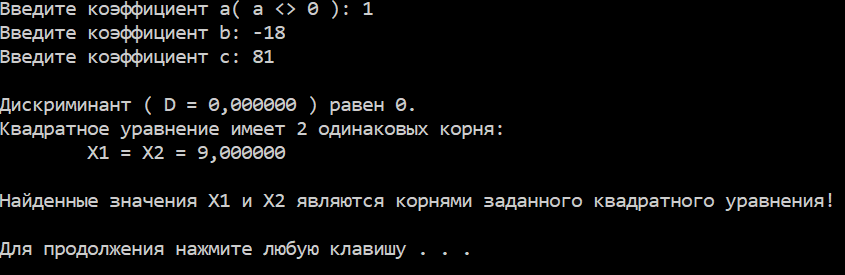
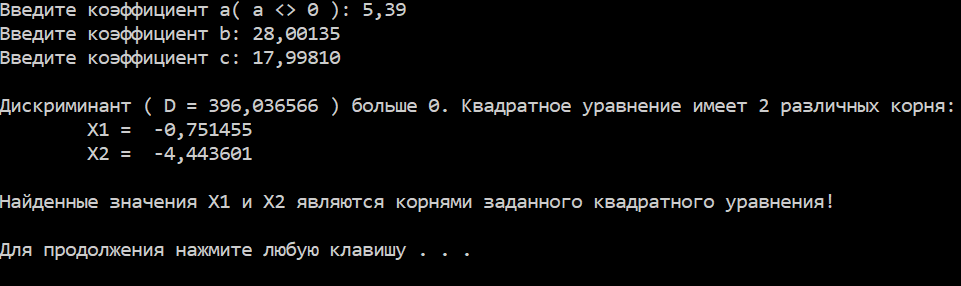
| ВНИМАНИЕ | Для получения программы своего варианта пишите на наш электронный адрес proglabs@mail.ru |
Добавить комментарий