Содержание
| ВНИМАНИЕ | Для получения программы своего варианта пишите на наш электронный адрес proglabs@mail.ru |
Уровень А
Постановка задания
Для бесконечного числового ряда
$a_1 + a_2 + … + a_n + … = \sum\limits_{n = 1}^\infty a_n$,
члены которого вычисляются по формуле, соответствующей индивидуальному варианту, вычислить сумму первых n членов ряда с использованием функции double Sum(int n).
Варианты заданий
| № | Формула ряда | № | Формула ряда |
| A1 | $a_n = \frac{1}{n^2\ +\ 10}$ | A2 | $a_n = \frac{1}{n^2\ +\ n}$ |
| A3 | $a_n = \frac{2}{n^2\ +\ 3}$ | A4 | $a_n = \frac{2}{n^2\ +\ 1}$ |
| A5 | $a_n = \frac{3}{n^2\ +\ 2n}$ | A6 | $a_n = \frac{1}{n^2\ +\ 2n\ +\ 1}$ |
| A7 | $a_n = \frac{n}{n^3\ +\ 1}$ | A8 | $a_n = \frac{n}{n^3\ +\ n\ +\ 1}$ |
| A9 | $a_n = \frac{n\ -\ 1}{n^3\ +\ 3}$ | A10 | $a_n = \frac{n\ +\ 1}{n^3\ +\ 1}$ |
| A11 | $a_n = \frac{n\ +\ 1}{n^3\ +\ 2n}$ | A12 | $a_n = \frac{n\ +\ 2}{n^3\ +\ 3}$ |
| A13 | $a_n = \frac{n\ -\ 3}{n^3\ -\ n\ +\ 1}$ | A14 | $a_n = \frac{n\ +\ 10}{n^3\ +\ 5n\ +\ 1}$ |
| A15 | $a_n = \frac{2}{n^3\ +\ n}$ | A16 | $a_n = \frac{3}{n^2\ -\ n\ +\ 1}$ |
| A17 | $a_n = \frac{10}{n^2\ +\ 5n\ +\ 1}$ | A18 | $a_n = \frac{1}{n^3\ — \ 3n}$ |
Уровень В
Постановка задания
Для бесконечного числового ряда
$a_1 + a_2 + … + a_n + … = \sum\limits_{n = 1}^\infty a_n$,
члены которого вычисляются по формуле, соответствующей индивидуальному варианту, вычислить приближенную сумму двумя способами: сумму первых n членов ряда и сумму с точностью до eps (эпсилон) в двух разных функциях:
- double Sum1(int n);
- double Sum2(double eps);
💡 Запрещается использовать функции pow() и условных операторов «if» и «? :»
Варианты заданий
| № | Формула ряда | № | Формула ряда |
| B1 | $a_n = (-1)^n \frac{n\ +\ 1}{n^3\ +\ 1}$ | B2 | $a_n = (-1)^n \frac{1}{n^2\ +\ 1}$ |
| B3 | $a_n = (-1)^n \frac{n}{n^3\ -\ n}$ | B4 | $a_n = (-1)^n \frac{1}{n^2\ +\ n\ +\ 2}$ |
| B5 | $a_n = (-1)^n \frac{n\ -\ 1}{n^4\ -\ n}$ | B6 | $a_n = (-1)^n \frac{n\ -\ 1}{n^3\ +\ n}$ |
| B7 | $a_n = (-1)^n \frac{n\ -\ 1}{n^3\ +\ 5n}$ | B8 | $a_n = (-1)^n \frac{1}{n^2\ +\ n\ -\ 1}$ |
| B9 | $a_n = (-1)^n \frac{n}{n^3\ -\ n\ +\ 2}$ | B10 | $a_n = (-1)^n \frac{n\ +\ 2}{n^3\ +\ n\ -\ 2}$ |
| B11 | $a_n = (-1)^n \frac{1}{n^2\ -\ n\ +\ 2}$ | B12 | $a_n = (-1)^n \frac{2}{n^2\ +\ n\ +\ 3}$ |
| B13 | $a_n = (-1)^n \frac{1}{n^4\ +\ 1}$ | B14 | $a_n = (-1)^n \frac{1}{n^3\ +\ n}$ |
| B15 | $a_n = (-1)^n \frac{n}{n^4\ +\ 1}$ | B16 | $a_n = (-1)^n \frac{n}{n^3\ -\ n\ +\ 1}$ |
| B17 | $a_n = (-1)^n \frac{1}{n^3\ +\ 10n}$ | B18 | $a_n = (-1)^n \frac{n}{n^3\ +\ n\ +\ 1}$ |
Уровень С
Постановка задания
Для функционального ряда
$a_1x + a_2x^2 + … + a_nx^n + … = \sum\limits_{n = 1}^\infty a_nx^n$,
коэффициенты которого вычисляются по формуле, соответствующей индивидуальному варианту, вычислить приближенную сумму при фиксированном значении х двумя способами: сумму первых n членов ряда и сумму с точностью до eps (эпсилон) в двух разных функция:
- double Sum1(double x, int n);
- double Sum2(double x, double eps).
💡 Запрещается использование условных операторов «if» и «? :», функции pow(), вторичное вычисление факториала и возведение в степень на каждом шаге итерации (использовать рекуррентные соотношения $n! = n \cdot (n — 1)!$, $a^n = a \cdot a^{n — 1}$).
Варианты заданий
| № | Формула ряда | № | Формула ряда |
| C1 | $a_n = (-1)^n \frac{n\ +\ 1}{3^n\ \cdot\ n!}$ | C2 | $a_n = (-1)^n \frac{n}{2^n\ \cdot\ (n\ -\ 1)!}$ |
| C3 | $a_n = (-1)^n \frac{2^n}{n!}$ | C4 | $a_n = (-1)^n \frac{n}{(n\ +\ 1)!}$ |
| C5 | $a_n = (-1)^n \frac{3^n}{(n\ -\ 1)!}$ | C6 | $a_n = (-1)^n \frac{n\ +\ 1}{(n\ -\ 1)!}$ |
| C7 | $a_n = (-1)^n \frac{n\ +\ 1}{2^n\ \cdot\ n!}$ | C8 | $a_n = (-1)^n \frac{n}{3^n\ \cdot\ (n\ +\ 1)!}$ |
| C9 | $a_n = (-1)^n \frac{3^n}{(n\ +\ 2)!}$ | C10 | $a_n = (-1)^n \frac{2^n}{3^{n\ +\ 1}\ \cdot\ (n\ +\ 1)!}$ |
Образец выполнения (вариант B4)
Условие задания
$a_n = (-1)^n \frac{1}{n^2\ +\ n\ +\ 2}$
Реализация задачи на языке Си
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 | #include <stdio.h> // консольный ввод-вывод #include <conio.h> // задержка программы #include <locale.h> // руссификация диалогов #include <math.h> // модуль вещественного числа // формула, по которой рассчитывается n-й член ряда double F(const int pn) { return 1.0 / (pn * pn + pn + 2); } // нахождение суммы первых n членов ряда double Sum1(int n) { int i; // номер члена ряда + счетчик цикла double s = 0; // сумма первых n членов ряда int sign = -1; // учет (-1)^n // в цикле получаем первых n членов ряда for(i = 1; i <= n; i++) { // добавляем текущий член ряда к сумму s += sign * F(i); sign = -sign; // учитываем в формуле (-1)^n } // в качестве ответа возвращаем сумму первых n членов ряда return s; } // нахождение суммы с точностью до заданной точности (eps) double Sum2(double eps) { int sign = -1; // учет (-1)^n double s = 0; // искомая сумма int i = 1; // номер члена ряда double current = sign * F(i); // значение текущего члена ряда // пока не достигнута заданная точность (модуль текущего члена не меньше заданной точности) while(fabs(current) >= eps) { s += current; // добавляем текущий член к сумме sign = -sign; // учитываем в формуле (-1)^n current = sign * F(++i); // перевычисляем текущий член ряда } // в качестве ответа возвращем сумму, рассчитанную до точности eps return s; } // главная функция программы (точка входа) int main(void) { int n; // количество первых n членов ряда double eps; // заданная точность setlocale(LC_ALL, ""); // руссификация диалогов // запрашиваем от пользователя количество членов ряда, из которых будет образована сумма printf("Введите натуральное n - количество членов ряда: "); scanf("%d", &n); printf("Сумма первых %d членов ряда составила: %0.6lf", n, Sum1(n)); // запрашиваем от пользователя точность вычислений, до которой будет рассчитана сумма printf("\n\nВведите точность вычисления EPS: "); scanf("%lf", &eps); printf("Сумма с заданной точностью составила: %0.6lf", Sum2(eps)); getch(); // имитация задержки программы, чтобы у пользователя была возможность просмотреть результат return 0; // завершение работы программы и передача управления в ОС } |
Результаты работы программы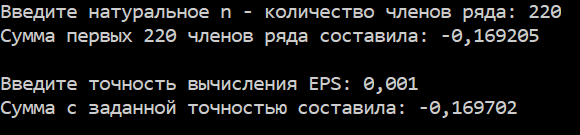
| ВНИМАНИЕ | Для получения программы своего варианта пишите на наш электронный адрес proglabs@mail.ru |
Добавить комментарий