Содержание
| ВНИМАНИЕ | Для получения программы своего варианта пишите на наш электронный адрес proglabs@mail.ru |
Постановка задания
Задание для всех вариантов звучит так (или, возможно, немного изменено, так как могут быть разные издания учебного пособия):
Для функции $f(x) = xe^x\ +\ 2sin(x)\ -\ \sqrt{|x^3\ -\ x^2|}$ составить программу построения таблицы значений функции при изменении аргумента от A = -5 до B = 5 с шагом H = 0.1. Значения A, B, H объявить как константы в директиве #define. В каждой строке выводить значение аргумента и соответствующее ему значение функции в форматированном виде с 4 знаками после запятой. Кроме того, в конце таблицы нужно напечатать отдельной строкой значение, которое требуется вычислить в соответствии с индивидуальным вариантом.
Варианты заданий (уровень А)
| № | Формулировка |
| А1 | Среднее арифметическое всех отрицательных значений функции. |
| А2 | Сумма таких значений функции, которые находятся на отрезке от M до N. |
| A3 | Среднее арифметическое таких значений функции, которые находятся на отрезке от M до N. |
| А4 | Среднее арифметическое таких значений функции, которые больше числа M. |
| А5 | Среднее арифметическое всех неотрицательных значений функции. |
| А6 | Количество всех отрицательных значений функции. |
| А7 | Количество таких значений функции, которые находятся на отрезке от M до N. |
| А8 | Количество всех неотрицательных значений функции. |
| А9 | Среднее арифметическое таких значений функции, которые меньше числа M. |
| А10 | Сумма таких значений функции $y = f(x)$, для которых выполнено неравенство $x > f(x)$. |
| A11 | Количество значений функции, которые меньше числа M. |
| A12 | Среднее арифметическое таких значений функции, которые меньше числа M. |
| A13 | Сумма таких значений функции, которые не принадлежат отрезку от M до N. |
| A14 | Количество таких значений функции $y = f(x)$, для которых выполнено неравенство $x < f(x)$. |
| A15 | Количество таких значений функции $y = f(x)$, для которых выполнено равенство $|x| = |f(x)|$. |
| A16 | Сумма таких значений функции $y = f(x)$, для которых выполнено неравенство $x^2 > f(x)$. |
| A17 | Сумма таких значений функции, которые по модулю больше числа M. |
Варианты заданий (уровень В)
| № | Формулировка |
| B1 | Количество отрицательных значений функции, имеющих нечетную целую часть. |
| B2 | Среднее арифметическое таких значений функции, которые имеют в младшем разряде целой части цифру, большую 3. |
| B3 | Среднее арифметическое таких значений функции, которые имеют дробную часть, меньшую 0.5. |
| B4 | Количество значений функции, имеющих в младшем разряде целой части цифру, большую 3. |
| B5 | Среднее арифметическое таких значений функции, которые имеют четную целую часть. |
| B6 | Количество неотрицательных значений функции, имеющих четную целую часть. |
| B7 | Сумма таких значений функции, которые имеют дробную часть, большую 0.5. |
| B8 | Сумма таких значений функции, которые имеют целую часть, кратную Z. |
| B9 | Среднее арифметическое таких значений функции, которые имеют нечетную целую часть. |
| B10 | Количество положительных значений функции, которые имеют четную целую часть и дробную часть, меньшую 0.5. |
| B11 | Сумма неотрицательных значений функции, которые имеют нечетную целую часть и дробную часть, большую 0.2. |
| B12 | Среднее арифметическое таких значений функции, которые имеют нечетную целую часть и дробную часть, большую 0.5. |
| B13 | Сумма таких значений функции, целая часть которых двузначна. |
| B14 | Количество таких значений функции, целая часть которых по модулю меньше числа М. |
| B15 | Сумма таких значений функции, дробная часть которых больше 0.3 и меньше 0.7. |
| B16 | Среднее арифметическое таких значений функции, целая часть которых по модулю больше числа М. |
| B17 | Среднее арифметическое таких значений функции, дробная часть которых больше 0.2 и меньше 0.8. |
Варианты заданий (уровень С)
| № | Формулировка |
| C1 | Минимальное среди неотрицательных значений функции и количество таких минимальных значений. |
| C2 | Максимальное среди значений функции, имеющих целую часть, кратную Z, и количество таких максимальных значений. |
| C3 | Минимальное среди значений функции, имеющих дробную часть, меньшую 0.5, и количество таких минимальных значений. |
| C4 | Минимальное среди значений функции, имеющих четную целую часть, и количество таких минимальных значений. |
| C5 | Максимальное среди значений функции, имеющих нечетную целую часть, и количество таких максимальных значений. |
| C6 | Максимальное среди значений функции, имеющих в младшем разряде целой части цифру, меньшую 4, и количество таких максимальных значений. |
| C7 | Максимальное среди значений функции, имеющих дробную часть больше 0.4, и количество таких максимальных значений. |
| C8 | Минимальное среди значений функции, которые имеют в младшем разряде целой части цифру, большую 3, и количество таких минимальных значений. |
| C9 | Минимальное среди значений функции, целая часть которых меньше числа М, и количество таких минимальных значений. |
| C10 | Максимальное среди значений функции, имеющих в младшем разряде целой части цифру, большую 2, и количество таких максимальных значений. |
Лабораторная работа №1 предполагает написание программы на языке Си. При заказе работы своего варианта вы получите качественно написанную и хорошо прокомментированную программу.
Образец выполнения (задание B1)
Условие задания
Количество отрицательных значений функции, имеющих нечетную целую часть.
Реализация задачи на языке Си
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 | #include <stdio.h> // для консольного вывода #include <math.h> // для математических функций #include <conio.h> // для задержки работы программы #include <locale.h> // для руссификации выводов #define A -5.0 // левая граница табулирования #define B 5.0 // правая граница табулирования #define H 0.1 // шаг табулирования // кодируем заданную функцию f(x) в терминах языка Си double F(const double px) { return px * exp(px) + 2 * sin(px) - sqrt(fabs(pow(px, 3) - pow(px, 2))); } // главная функция всей программы (точка входа) int main(void) { int n; // количество разбиений отрезка табулирования функции int i; // счетчик цикла (номер итерации) double x; // значение аргумента функции double y; // значение функции f(x) double integerPart; // целая часть значения функции double fractionalPart; // дробная часть значения функции int count = 0; // кол-во отрицательных значений функции, имеющих нечетную целую часть // руссификация выводов сообщений на экран setlocale(LC_ALL, "rus"); n = (B - A) / H; // определяем количество разбиений отрезка табулирования функции [A .. B] // выводим шапку таблицы printf("\tx\t\tf(x)\n"); printf(" -----------------------------\n"); // начинается процесс табулирования функции f(x) for(i = 0; i <= n; i++) { x = A + H * i; // вычисляем значение аргумента функции f(x) y = F(x); // вычисляем значение функции в точке x // выводим на экран значение аргумента и значение функции printf("%12.4lf\t%12.4lf\n", x, y); // получаем целую и дробную часть текущего значения функции fractionalPart = modf(y, &integerPart); // если значение функции отрицательно и одновременно с этим целая часть этого значения является нечетной величиной if((y < 0) && ((int)fabs(integerPart) % 2 == 1)) count++; // увеличиваем счетчик искомых значений на +1 } // выводим на экран количество значений, удовлетворяющих заданным условиям printf("\nКоличество отрицательных значений функции, имеющих нечетную целую часть: %d", count); getch(); // имитация задержки работы программы, чтобы у пользователя была возможность просмотреть результат return 0; // завершение работы программы и передача управления в ОС } |
Результаты работы программы
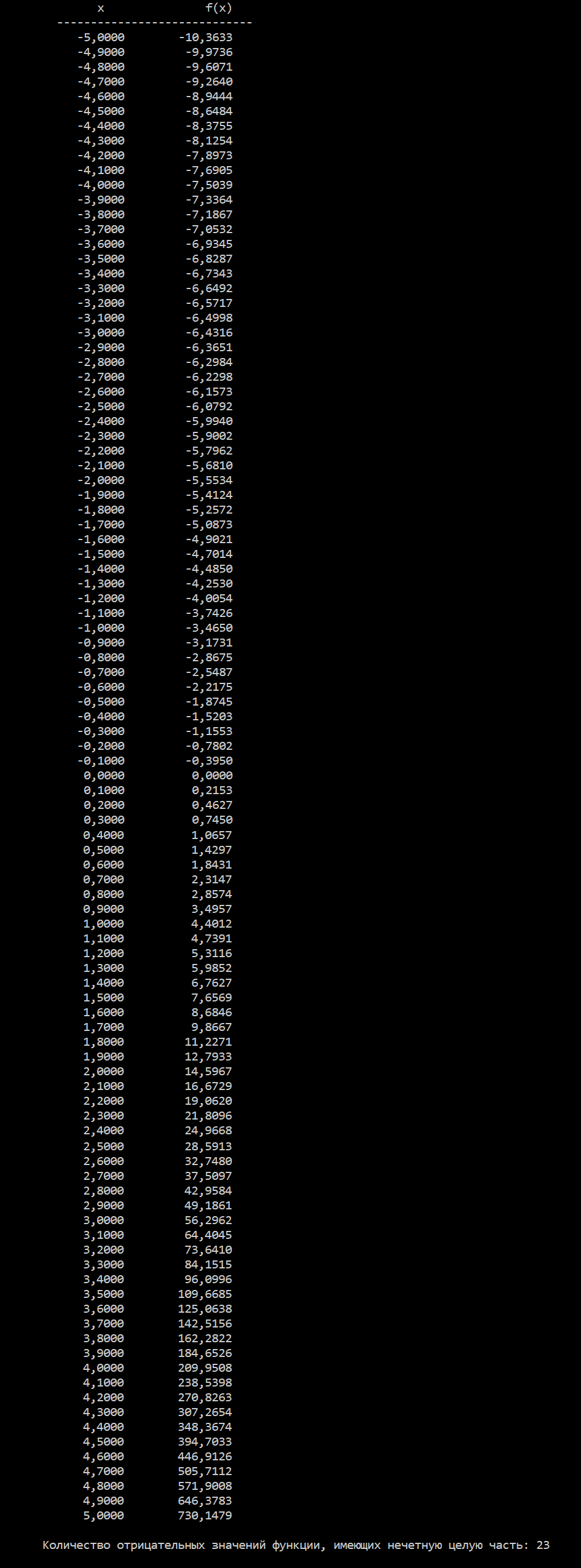
| ВНИМАНИЕ | Для получения программы своего варианта пишите на наш электронный адрес proglabs@mail.ru |
Добавить комментарий